
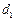 和
和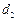 为公差的等差数列
为公差的等差数列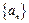 和
和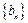 满足
满足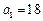 ,
, 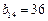 ,
,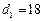 ,
, 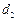 ≥2917,且
≥2917,且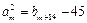 ,求
,求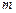 的取值范围;
的取值范围;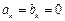 ,且数列
,且数列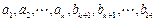 …的前
…的前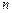 项和
项和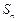 满足
满足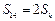 ,
,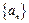 和
和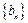 的通项公式;
的通项公式;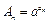 ,
,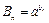 ,
, 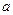 >0且
>0且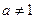 ,探究不等式
,探究不等式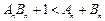 是否对一切正整数
是否对一切正整数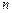 恒成立?
恒成立?科目:高中数学 来源:不详 题型:解答题
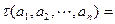
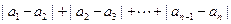 为有限项数列
为有限项数列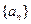 的波动强度.
的波动强度.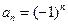 时,求
时,求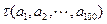 ;
;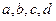 满足
满足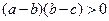 ,求证:
,求证: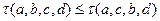 ;
;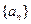 各项均不相等,且交换数列
各项均不相等,且交换数列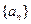 中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列
中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列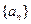 一定是递增数列或递减数列
一定是递增数列或递减数列查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
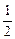 .
.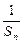 }是等差数列;
}是等差数列;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
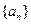 满足
满足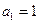 ,
,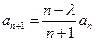 ,其中
,其中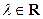 ,
,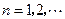 .给出下列命题:
.给出下列命题: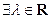 ,对于任意
,对于任意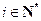 ,
,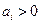 ;
;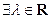 ,对于任意
,对于任意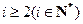 ,
,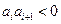 ;
;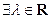 ,
,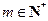 ,当
,当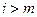 (
(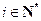 )时总有
)时总有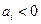 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com