
已知函数f(x)=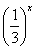 ,x∈[-1,1],函数
,x∈[-1,1],函数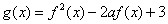 的最小
的最小
值为h(a).
(1)求h(a)的解析式;(7分)
(2)是否存在实数m,n同时满足下列两个条件:①m>n>3;②当h(a)的定义域
为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,请说明理由.(14分)
解:(1)由f(x)=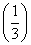 x,x∈[-1,1],知f(x)∈
x,x∈[-1,1],知f(x)∈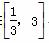 ,令t=f(x)∈
,令t=f(x)∈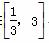
记g(x)=y=t2-2at+3,则g(x)的对称轴为t=a,故有:
①当a≤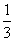 时,g(x)的最小值h(a)=
时,g(x)的最小值h(a)=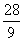 -
-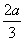 ,
,
②当a≥3时,g(x)的最小值h(a)=12-6a,
③当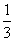 <a<3时,g(x)的最小值h(a)=3-a2
<a<3时,g(x)的最小值h(a)=3-a2
综上所述,h(a)=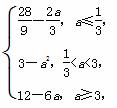
(2)当a≥3时,h(a)=-6a+12,故m>n>3时,h(a)在[n,m]上为减函数,
所以h(a)在[n,m]上的值域为[h(m),h(n)].
由题意,则有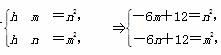 ,两式相减得6n-6m=n2-m2,又m≠n,所以m+n=6,这与
,两式相减得6n-6m=n2-m2,又m≠n,所以m+n=6,这与
m>n>3矛盾,故不存在满足题中条件的m,n的值.


科目:高中数学 来源: 题型:
假设你家订了一份报纸,送报人可能在早上630—730之间把报纸送到你家,你父亲离开家去工作的时间在早上700—800之间,问你父亲在离开家前能得到报纸(称为事件A)的概率是_______________
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)是定义在R上的增函数,且对于任意的x都有f(-x)+f(x)=0恒成立.如果实
数m、n满足不等式f(m2-6m+21)+f(n2-8n)<0,那么m2+n2的取值范围是( A )
A.(9,49) B.(13,49) C.(9,25) D.(3,7)
查看答案和解析>>
科目:高中数学 来源: 题型:
某商店为了吸引顾客,设计了一个摸球小游戏,顾客从装有1个红球,1个白球,3个黑球的袋中一次随机的摸2个球,设计奖励方式如下表:
| 结果 | 奖励 |
| 1红1白 | 10元 |
| 1红1黑 | 5元 |
| 2黑 | 2元 |
| 1白1黑 | 不获奖 |
(1)某顾客在一次摸球中获得奖励X元,求X的概率分布表与数学期望;
(2)某顾客参与两次摸球,求他能中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com