
若z+![]() 是实数, 且│z-2│=
是实数, 且│z-2│=![]() , 则复数z=
, 则复数z=![]() ±
±![]() i或z=2±
i或z=2±![]()
( )
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
. |
| z |
. |
| z |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高二下学期数学单元测试2-理科 题型:解答题
满足z+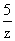 是实数,且z+3的实部与虚部互为相反数的虚数z是否存在,若存在,求出虚数z;若不存在,请说明理由.
是实数,且z+3的实部与虚部互为相反数的虚数z是否存在,若存在,求出虚数z;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com