
| A. | ③④ | B. | ①②④⑤ | C. | ①③④⑤ | D. | ①②③④⑤ |
分析 ①对任意命题的否定,应把任意改为存在一个,再把结论否定,
②求出非命题,利用四种命题的等价关系得出¬p⇒¬q,可得q⇒p;
③⑤可直接由定义判定;
④“在三角形ABC中,根据大角对大边,A>B,结合正弦定理可得结论.
解答 解:①对任意命题的否定,应把任意改为存在一个,再把结论否定,故正确;
②∵命题q:x+y≠5,命题p:x≠2或y≠3,
∴命题¬q:x+y=5,命题¬p:x=2且y=3,
∴¬p是¬q的充分不必要条件,
∴q⇒p,
即p是q的必要不充分条件,故正确;
③数列{an}满足“an+1=3an”可推出“数列{an}为等比数列”,
但“数列{an}为等比数列”,不一定公比为3,故应是充分不必要条件,故错误;
④“在三角形ABC中,根据大角对大边,A>B,
∴a>b,由正弦定理知sinA>sinB,故正确;
⑤由否命题的定义可知正确.
故选B.
点评 考查了四种命题的逻辑关系和任意命题的否定.属于基础题型,用牢记.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
 在四棱锥S一ABCD中,底面ABCD为正方形,S在底面的射影为底面中心O,且SA=SB=SC=SD=AB=2,以O为坐际原点建立如图所示的空间直角坐标系.
在四棱锥S一ABCD中,底面ABCD为正方形,S在底面的射影为底面中心O,且SA=SB=SC=SD=AB=2,以O为坐际原点建立如图所示的空间直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 100g食物 | 碳水化合物/g | 蛋白质/g | 脂肪/g |
| A | |||
| B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
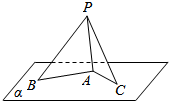 如图所示,8m高旗杆PA直立在地面α上,拉绳PB与地面α成30°的角,拉绳PC在地面α上的射影AC的长是8m.求:
如图所示,8m高旗杆PA直立在地面α上,拉绳PB与地面α成30°的角,拉绳PC在地面α上的射影AC的长是8m.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com