练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知一个高度不限的直三棱柱ABC-A1B1C1，AB=4，BC=5，CA=6，点P是侧棱AA1上一点，过A作平面截三棱柱得截面ADE，给出下列结论：①△ADE是直角三角形；②△ADE是等边三角形；③四面体APDE为在一个顶点处的三条棱两两垂直的四面体．其中有不可能成立的结论的个数是（　　）
    A．0B．1C．2D．3

    分析 因为是高度不限，所以①②都可能成立；③可对四个顶点分别讨论，用反证法逐个得出矛盾，得出结论．

    解答 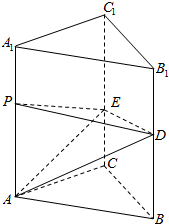解：如图，做直三棱柱ABC-A1B1C1，AB=4，BC=5，CA=6，
    ①不妨取AD=6，AE=10，DE=8，则△ADE是直角三角形，①可能成立；
    ②不妨令AD=AE=DE=a（a＞6），则△ADE是等边三角形，②可能成立；
    ③假设四面体APDE为在一个顶点处的三条棱两两垂直的四面体，
    当A为直角顶点时，在直三棱柱ABC-A1B1C1中，PA⊥底面ABC，则 E，D分别与C，B重合，此时，∠EAD不是直角，与假设矛盾，假设不成立，
    当P为直角顶点时，可得PD∥AB，PE∥AC，由等角定理知则∠EPD不可能是直角，与假设矛盾，假设不成立，
    当E或D点为直角顶点时，不妨选E为直角顶点，则DE⊥EP，DE⊥EA，EP∩EA═A，EP?平面ACC1A1，EA?平面ACC1A1，
    则平面ACC1A1与平面BCC1B1垂直，则直三棱柱ABC-A1B1C1中，可证∠ACB为二面角的平面角，∠ACB═90°，与题意矛盾，假设不成立．
    综上③错误．
    故选：B．

    点评 考查了空间几何体的线面平行，垂直的应用．难点是③的分类判断．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．如图所示，ABCD是正方形，CC1⊥平面ABCD，且DD1∥BB1∥CC1，菱形AB1C1D1中，∠D1C1B1=α．
    （1）求证：BD∥平面AB1C1D1
    （2）若直线AC1与平面ABCD所成的角为θ，求证：cosθ=tan$\frac{α}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．如图，ABCD是矩形，PA⊥平面ABCD，PA=AD=a，AB=$\sqrt{2}$A，E是线段PD上的点，F是线段AB上的点，且$\frac{PE}{ED}$=$\frac{BF}{FA}$=$\frac{1}{2}$，求直线EF与平面ABCD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知P是△ABC所在平面外的一点，PA、PB、PC两两垂直，且P在△ABC所在平面内的射影H在△ABC内，则H一定是△ABC的垂心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．给出下列结论：①命题“?x∈R，sinx≠1”的否定是“?x∈R，sinx=1”；②命题p：x≠2或y≠3，命题q：x+y≠5则p是q的必要不充分条件；③数列{an}满足“an+1=3an”是“数列{an}为等比数列”的充分必要条件；④“在三角形ABC中，若sinA＞sinB，则A＞B”的逆命题是真命题；⑤“若a＞b，则2a＞2b-1”的否命题为“若a≤b，则2a≤2b-1”．其中正确的是（　　）
    A．③④B．①②④⑤C．①③④⑤D．①②③④⑤

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知抛物线C：y2=2px（p＞0），焦点为F，准线为l，抛物线C上一点A的横坐标为3，且点A到准线l的距离为5．
    （1）求抛物线C的方程；
    （2）若P为抛物线C上的动点，求线段FP的中点M的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．给出下列四种说法，说法正确的有①③（请填写序号）
    ①函数y=ax（a＞0，且a≠1）与函数y=logaax（a＞0，且a≠1）的定义域相同；
    ②函数f（x）=$\sqrt{{x^2}-1}+\sqrt{1-{x^2}}$和y=$\sqrt{x-1}+\sqrt{1-x}$都是既奇又偶的函数；
    ③已知对任意的非零实数x都有$f（x）+2f（\frac{1}{x}）=2x+1$，则f（2）=-$\frac{1}{3}$；
    ④函数f（x）在（a，b]和（b，c）上都是增函数，则函数f（x）在（a，c）上一定是增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．对于任意实数a、b、c、d，命题：
    ①若a＞b，则$\frac{1}{a}$＜$\frac{1}{b}$；
    ②若a＞b，c＞d，则a-c＞b-d；
    ③若ac2＞bc2，则a＞b；
    ④若a＞b＞0，c＞d，则ac＞bd．
    其中真命题的个数是（　　）
    A．0B．2C．1D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知△ABC中，∠C为直角，D为边AC上一点，K为BD上一点，且∠ABC=∠KAD=∠AKD．证明：BK=2DC．

    查看答案和解析>>

    同步练习册答案