
以点(-2,3)为圆心且与y轴相切的圆的方程是 .
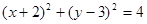
【解析】
试题分析:圆心C的坐标为(-2,3),且所求圆与y轴相切,
∴圆的半径r=|-2|=2,
则所求圆的方程为(x+2)2+(y-3)2=4.
故答案为:(x+2)2+(y-3)2=4
考点:本题主要是考查直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,当直线与圆相切时,圆心到直线的距离等于圆的半径,
点评:解决该试题的关键是其中根据题意得到圆心横坐标的绝对值为圆的半径.要求圆的方程,注意找出圆心和半径,而圆心已知,故要求圆的半径,方法为:由所求圆与y轴相切,得到圆心的横坐标的绝对值为圆的半径,进而由圆心C的坐标和求出的半径写出圆的标准方程即可.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源:北京市西城区2012届高三4月第一次模拟考试数学文科试题 题型:044
已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,一个焦点为F(2
,一个焦点为F(2![]() ,0).
,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx-![]() 交椭圆C于A,B两点,若点A,B都在以点M(0,3)为圆心的圆上,求k的值.
交椭圆C于A,B两点,若点A,B都在以点M(0,3)为圆心的圆上,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
以点P(-4,3)为圆心的圆与直线2x+y-5=0相离,则圆P的半径r的取值范围是( )
A.(0,2) B.(0,![]() )
)
C.(0,2![]() ) D.(0,10)
) D.(0,10)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com