
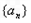 ,a1=1,
,a1=1,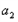
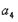 =16,单调增数列
=16,单调增数列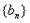 的前n项和为
的前n项和为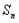 ,
,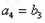 ,且
,且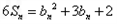 (
(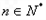 ).
).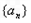 、
、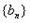 的通项公式;
的通项公式;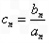 (
(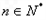 ),求使得
),求使得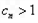 的所有n的值,并说明理由.
的所有n的值,并说明理由.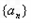 中任意三项不可能构成等差数列.
中任意三项不可能构成等差数列.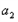
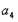 =
=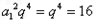 ,
,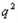 =4,
=4,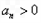 ,
,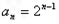
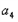 =8.
=8. 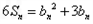 +2①
+2①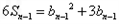 +2 ②
+2 ②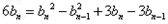
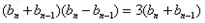
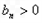
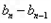 =3,
=3,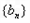 是公差为3的等差数列.
是公差为3的等差数列.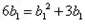 +2,解得
+2,解得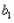 =1或
=1或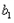 =2,
=2,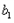 =1时,
=1时,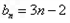 ,此时
,此时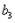 =7,与
=7,与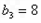 矛盾;
矛盾;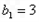 时
时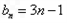 ,此时此时
,此时此时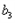 =8=
=8=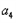 ,
,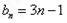 .
. 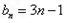 ,
,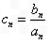 =
=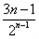 ,
,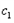 =2>1,
=2>1,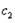 =
=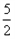 >1,
>1,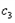 =2>1,
=2>1,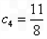 >1,
>1,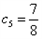 <1,
<1,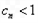
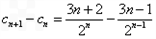 =
=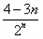 <0即
<0即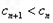 ,
,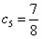 <1
<1 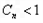 ,
,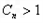 的所有n的值为1,2,3,4.
的所有n的值为1,2,3,4. 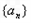 中存在三项p,q,r (p<q<r,p,q,R∈N*)使ap, aq, ar构成等差数列,
中存在三项p,q,r (p<q<r,p,q,R∈N*)使ap, aq, ar构成等差数列,

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源:云南省昆明市东川高级中学2009-2010学年高二数学上期期中质量检测试题 题型:013
各项均为正数的等比数例{an}的前n项和为Sn,若Sn=2,S3n=14,则S4n等于
16
26
30
80
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com