����֤�����������n��N*���У�1+2+��+n��2=13+23+��+n3���������波���ƹ�����⣺
��1������������ɵ�����a1��a2��a3ÿ������㣬�Ҷ������n��{1��2��3}�У�a1+a2+��+an��2=a13+a23+��+an3�������������������������У�
��2��������{an}ÿ������㣬�Ҷ������n��N*�У�a1+a2+��+an��2=a13+a23+��+an3����������{an}��ǰn���ΪSn����֤��an+12-an+1=2Sn��n��N*��
��3���Ƿ�������㣨2������������������{an}��ʹ��a2012=-2011�������ڣ�д��һ���������������У�����Ҫ֤���������������� �������ڣ�˵�����ɣ�
���𰸡�
��������1�����ã�a
1+a
2+��+a
n��
2=a
13+a
23+��+a
n3���ֱ�ȡn=1��2��3������⼴�ɣ�
��2������֪��n��2ʱ��a
13+a
23+��+a
n3=S
n2��a
13+a
23+��+a
n-13=S
n-12����ʽ����������֤��
��3�����ڣ�
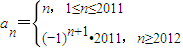
��һ�������������������У�
����⣺��1��ȡn=1��a
12=a
13����a
1��0����a
1=1
ȡn=2���У�1+a
2��
2=1+a
23����a
2=-1��2
��a
2=-1ʱ��ͬ����a
3=1��
��a
2=2ʱ��ͬ����a
3=3��-2
����֪��������������˼ά����Ϊ1��-1��1��1��2��3��1��2��-2��
��2������֪��n��2ʱ��a
13+a
23+��+a
n3=S
n2��
a
13+a
23+��+a
n-13=S
n-12��
��ʽ���֪��a
n3=S
n2-S
n-12=a
n��2a
1+2a
2+��+2a
n-1+a
n����
��a
n��0
��a
n2=2a
1+2a
2+��+2a
n-1+2a
n-a
n��a
n2=2S
n-a
n��a
n+12-a
n+1=2S
n��n��N
*��
��3�����ڣ�
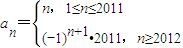
��һ�������������������У�
��������������֪����Ϊǰ�ᣬ�����ƹ������⣬���鸳ֵ�����ڽ��Ĺ��̵��г������������ͨ����ǰn��͵�֪ʶ��

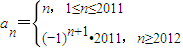 ��һ�������������������У�
��һ�������������������У�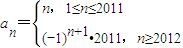 ��һ�������������������У�
��һ�������������������У�


