�⣺��I�������ܵ����ڵ������߷���Ϊf��x��=a
0x
2+b
0x+c
0��
������֪
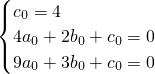
���a
0=1��b
0=-4��c
0=4��
�����ܵ����ڵ������߷���Ϊy=x
2-4x+4��
��II������й켣���������߷���Ϊg��x��=ax
2+bx+c����a��0��
������֪
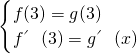
����
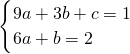
�����
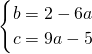
��g��x��=ax
2+��2-6a��x+9a-5=a��x-
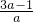
��
2+1-

��
��g��x��=1���ã�x-
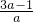
��
2=

��
��a��0����x=
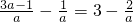
��
��x=
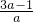
ʱ��g��x�������ֵ1-

��
���˶�Ա���о���d=3-

-3=-

�����й����о���ƽ̨���߶�h=1-

-1=-

��
������4��-

��6����2��-

��3��
���й����о���ƽ̨���߶ȵ�ȡֵ��Χ��2��3��֮�䣮
��������1�������ܵ����ڵ������߷���Ϊf��x��=a
0x
2+b
0x+c
0�������⣬���ܵ�һ�˵�A��0��4������һ�˵�C��3��1������B��2��0�����ó������飬�ɴ�����������
��2������й켣���������߷���Ϊg��x��=ax
2+bx+c����a��0����������֪
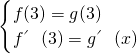
���ɴ����������g��x�������ֵ���÷��й����о���ƽ̨���߶ȣ����ò��ȹ�ϵ���ɵó��˶�Ա���й����о���ƽ̨���߶ȵ�ȡֵ��Χ��
���������⿼�������߷��̵�����������������ʵ����ȡֵ��Χ��������ʱҪ�������⣬��ϸ���ע��ȼ�ת��˼��ĺ������ã�

 �ֻ��Ǵ��Ŵ����ֵ�����Ь�ڼ�Ӳ�ij����ϻ��е��˶�����ͼ�����ܵ�ABC��һ�������ߣ�ij�ֻ��˶�Աͨ�����ܵ���ȡ�ٶȺ�����ܵ�Ȼ���䵽������Ϊ1��ƽ̨��E�������еĹ켣��һ��������CDE��������CDE��������ABC��ͬһƽ���ڣ���DΪ��������ߵ���ߵ㣮�����˶�Ա�Ļ��й켣����ƽ���Ͻ�����ͼ��ʾ��ֱ������ϵ��x���ڵ����ϣ����ܵ�һ�˵�A��0��4������һ�˵�C��3��1������B��2��0������λ���ף�
�ֻ��Ǵ��Ŵ����ֵ�����Ь�ڼ�Ӳ�ij����ϻ��е��˶�����ͼ�����ܵ�ABC��һ�������ߣ�ij�ֻ��˶�Աͨ�����ܵ���ȡ�ٶȺ�����ܵ�Ȼ���䵽������Ϊ1��ƽ̨��E�������еĹ켣��һ��������CDE��������CDE��������ABC��ͬһƽ���ڣ���DΪ��������ߵ���ߵ㣮�����˶�Ա�Ļ��й켣����ƽ���Ͻ�����ͼ��ʾ��ֱ������ϵ��x���ڵ����ϣ����ܵ�һ�˵�A��0��4������һ�˵�C��3��1������B��2��0������λ���ף�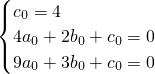
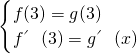 ����
����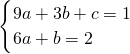 �����
�����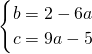
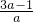 ��2+1-
��2+1- ��
��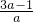 ��2=
��2= ��
��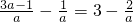 ��
��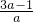 ʱ��g��x�������ֵ1-
ʱ��g��x�������ֵ1- ��
�� -3=-
-3=- �����й����о���ƽ̨���߶�h=1-
�����й����о���ƽ̨���߶�h=1- -1=-
-1=- ��
�� ��6����2��-
��6����2��- ��3��
��3��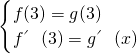 ���ɴ����������g��x�������ֵ���÷��й����о���ƽ̨���߶ȣ����ò��ȹ�ϵ���ɵó��˶�Ա���й����о���ƽ̨���߶ȵ�ȡֵ��Χ��
���ɴ����������g��x�������ֵ���÷��й����о���ƽ̨���߶ȣ����ò��ȹ�ϵ���ɵó��˶�Ա���й����о���ƽ̨���߶ȵ�ȡֵ��Χ��

 ��У����ϵ�д�
��У����ϵ�д�
 ij�������һ���ⳤΪ
ij�������һ���ⳤΪ ��5•12���봨������ǻ���������Զ��ʹ�����ֺ��ؽ������ھ�������ABCD�ڽ�һ���Σ���ԭ��λһ�������봨�������㳡����ͼ��������AEF�ڲ���һ������Ϊ���ﱣ��������ռ�ã�������AB=100m��BC=80m��AE=30m��AF=20m�������Ʋ���ʹ�㳡������
��5•12���봨������ǻ���������Զ��ʹ�����ֺ��ؽ������ھ�������ABCD�ڽ�һ���Σ���ԭ��λһ�������봨�������㳡����ͼ��������AEF�ڲ���һ������Ϊ���ﱣ��������ռ�ã�������AB=100m��BC=80m��AE=30m��AF=20m�������Ʋ���ʹ�㳡������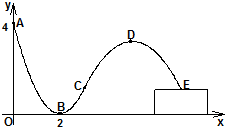 �ֻ��Ǵ��Ŵ����ֵ�����Ь�ڼ�Ӳ�ij����ϻ��е��˶�����ͼ�����ܵ�ABC��һ�������ߣ�ij�ֻ��˶�Աͨ�����ܵ���ȡ�ٶȺ�����ܵ�Ȼ���䵽������Ϊ1��ƽ̨��E�������еĹ켣��һ��������CDE��������CDE��������ABC��ͬһƽ���ڣ���DΪ��������ߵ���ߵ㣮�����˶�Ա�Ļ��й켣����ƽ���Ͻ�����ͼ��ʾ��ֱ������ϵ��x���ڵ����ϣ����ܵ�һ�˵�A��0��4������һ�˵�C��3��1������B��2��0������λ���ף�
�ֻ��Ǵ��Ŵ����ֵ�����Ь�ڼ�Ӳ�ij����ϻ��е��˶�����ͼ�����ܵ�ABC��һ�������ߣ�ij�ֻ��˶�Աͨ�����ܵ���ȡ�ٶȺ�����ܵ�Ȼ���䵽������Ϊ1��ƽ̨��E�������еĹ켣��һ��������CDE��������CDE��������ABC��ͬһƽ���ڣ���DΪ��������ߵ���ߵ㣮�����˶�Ա�Ļ��й켣����ƽ���Ͻ�����ͼ��ʾ��ֱ������ϵ��x���ڵ����ϣ����ܵ�һ�˵�A��0��4������һ�˵�C��3��1������B��2��0������λ���ף�