解:(Ⅰ)依题意知,半焦距c=2

,由点M(2

,1)在椭圆C上,得|MF
2|=1,|MF
1|=7;∴2a=|MF
1|+|MF
2|=8;∴a=4,∴b
2=a
2-c
2=4;所以,椭圆C的方程为:

+

=1.
(Ⅱ)设PQ的中点为R,直线l的方程为y=-x+m;
由
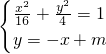
,得5x
2-8mx+4m
2-16=0(*);
要使l与椭圆C相交于不同的P、Q两点,则有△>0;
∴△=(-8m)
2-4×5(4m
2-16)=16(-m
2+20)>0,
化简,得|m|<2

. ①
由(*)知:x
R=

=

m,y
R=-x
R+m=

m.
且|BP|=|BQ|,所以BR⊥PQ,即k
RQ•(-1)=-1;
所以
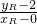
=
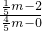
=1,解得m=-

.
因为

<2

,所以m=-

适合①.
所以存在满足条件的直线l;y=-x-

.
分析:(Ⅰ)由半焦距c=2

,点M(2

,1)在椭圆C上,可得|MF
2|,|MF
1|;由|MF
1|+|MF
2|=2a,可得a的值,从而得椭圆C的方程.
(Ⅱ)设PQ的中点为R,直线l的方程为y=-x+m;由
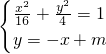
,得5x
2-8mx+4m
2-16=0(*);要使l与椭圆C相交于不同的P、Q两点,则有△>0,可得|m|<2

①,由(*)和中点坐标知x
R,y
R;且|BP|=|BQ|,得BR⊥PQ,即得k
RQ的值;从而解得m的值,得满足条件的直线l.
点评:本题考查了直线与椭圆标准方程的综合应用问题,解题时要弄清题中所给的条件,灵活运用椭圆的定义,根与系数的关系式,以及中点坐标公式来进行求解.

 ,1)在椭圆C:
,1)在椭圆C: +
+ =1(a>b>0)上,椭圆的两个焦点F1(-2
=1(a>b>0)上,椭圆的两个焦点F1(-2 ,0)和F2(2
,0)和F2(2 ,0),斜率为-1的直线l与椭圆C相交于不同的P、Q两点.
,0),斜率为-1的直线l与椭圆C相交于不同的P、Q两点. ,由点M(2
,由点M(2 ,1)在椭圆C上,得|MF2|=1,|MF1|=7;∴2a=|MF1|+|MF2|=8;∴a=4,∴b2=a2-c2=4;所以,椭圆C的方程为:
,1)在椭圆C上,得|MF2|=1,|MF1|=7;∴2a=|MF1|+|MF2|=8;∴a=4,∴b2=a2-c2=4;所以,椭圆C的方程为: +
+ =1.
=1.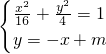 ,得5x2-8mx+4m2-16=0(*);
,得5x2-8mx+4m2-16=0(*); . ①
. ① =
= m,yR=-xR+m=
m,yR=-xR+m= m.
m.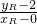 =
=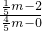 =1,解得m=-
=1,解得m=- .
. <2
<2 ,所以m=-
,所以m=- 适合①.
适合①.  .
. ,点M(2
,点M(2 ,1)在椭圆C上,可得|MF2|,|MF1|;由|MF1|+|MF2|=2a,可得a的值,从而得椭圆C的方程.
,1)在椭圆C上,可得|MF2|,|MF1|;由|MF1|+|MF2|=2a,可得a的值,从而得椭圆C的方程.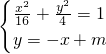 ,得5x2-8mx+4m2-16=0(*);要使l与椭圆C相交于不同的P、Q两点,则有△>0,可得|m|<2
,得5x2-8mx+4m2-16=0(*);要使l与椭圆C相交于不同的P、Q两点,则有△>0,可得|m|<2 ①,由(*)和中点坐标知xR,yR;且|BP|=|BQ|,得BR⊥PQ,即得kRQ的值;从而解得m的值,得满足条件的直线l.
①,由(*)和中点坐标知xR,yR;且|BP|=|BQ|,得BR⊥PQ,即得kRQ的值;从而解得m的值,得满足条件的直线l.

 在平面直角坐标系中,点P(x,y)满足约束条件:
在平面直角坐标系中,点P(x,y)满足约束条件: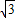 ,1)在椭圆C:
,1)在椭圆C: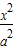 +
+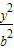 =1(a>b>0)上,椭圆的两个焦点F1(-2
=1(a>b>0)上,椭圆的两个焦点F1(-2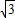 ,0)和F2(2
,0)和F2(2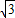 ,0),斜率为-1的直线l与椭圆C相交于不同的P、Q两点.
,0),斜率为-1的直线l与椭圆C相交于不同的P、Q两点.