
分析 (1)将式子分母有理化得到$\frac{3+\sqrt{5}}{2}$,估计$\sqrt{5}$的取值范围确定出整数部分A的值,即可求得小数部分B的值;
(2)将A和B代入A2+B2+$\frac{1}{2}$AB即可求得其值;
(3)由数列B,B2,B3,…,Bn为首项为B公比B的等比数列,利用等比数列前n项和公式求得B+B2+…+Bn,根据B的取值范围,即可求得$\underset{lim}{n→∞}$(1+B+B2+…+Bn)的值.
解答 解:(1)∵2<$\sqrt{5}$<3,
而设m=$\frac{\sqrt{5}+1}{\sqrt{5}-1}$=$\frac{3+\sqrt{5}}{2}$,
∴2<2m-3<3,
解得:2.5<m<3,
则:A=2,B=m-2=$\frac{\sqrt{5}-1}{2}$,
(2)将A=2,B=m-2=$\frac{\sqrt{5}-1}{2}$,代入得:
A2+B2+$\frac{1}{2}$AB=4+($\frac{\sqrt{5}-1}{2}$)2+$\frac{\sqrt{5}-1}{2}$=5;
(3)数列B,B2,B3,…,Bn为首项为B公比B的等比数列,
∵0<B<1,
∴前n项和$\frac{B(1-{B}^{n})}{1-B}$,
$\underset{lim}{n→∞}$(1+B+B2+…+Bn)=$\underset{lim}{n→∞}$(1+$\frac{B(1-{B}^{n})}{1-B}$)=$\frac{1}{1-B}$,
∴$\underset{lim}{n→∞}$(1+B+B2+…+Bn)=$\frac{1}{1-B}$.
点评 本题考查求得等比数列前n项和公式,考查数列极限的定义及意义,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
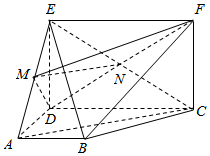 如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.
如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD,BE⊥DF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com