
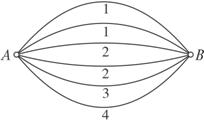
(1)设选取的三条网线由A到B可通过的信息总量为X,当X≥6时,则保证信息畅通,求线路信息畅通的概率.
(2)求选取的三条网线可通过信息总量的期望是多少.
分析:先分析X的所有可能取值,然后求出X取每一个值的概率,进而列出分布列.
解:X的所有可能取值为4,5,6,7,8,9.
当X=4时,有1+1+2=4,
∴P(X=4)=![]()
当X=5时,有1+1+3=1+2+2=5,
∴P(X=5)=![]() .
.
当X=6时,有1+1+4=1+2+3=6,
∴P(X=6)=![]() .
.
当X=7时,有1+2+4=2+2+3=7,
∴P(X=7)=![]() .
.
当X=8时,有1+3+4=2+2+4=8,
∴P(X=8)=![]() .
.
当X=9时,有2+3+4=9,
∴P(X=9)=![]() .
.
X | 4 | 5 | 6 | 7 | 8 | 9 |
P |
|
|
|
|
|
|
(1)P(X≥6)=P(X=6)+P(X=7)+P(X=8)+P(X=9)=![]() +
+![]() +
+![]() +
+![]() =
=![]() .
.
(2)线路通过信息量的数学期望EX=4×![]() +5×
+5×![]() +6×
+6×![]() +7×
+7×![]() +8×
+8×![]() +9×
+9×![]() =6.5.
=6.5.
绿色通道:本题求X的分布列是关键,而求X取每一个值时的概率综合了排列组合的有关知识.


科目:高中数学 来源: 题型:
 (2012•佛山二模)如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
(2012•佛山二模)如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°、45°,且A、B两点之间的距离为60m,则树的高度为( )
如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°、45°,且A、B两点之间的距离为60m,则树的高度为( )查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•广州二模)如图,A,B两点之间有4条网线连接,每条网线能通过的最大信息量分别为1,2,3,4.从中任取两条网线,则这两条网线通过的最大信息量之和为5的概率是
(2012•广州二模)如图,A,B两点之间有4条网线连接,每条网线能通过的最大信息量分别为1,2,3,4.从中任取两条网线,则这两条网线通过的最大信息量之和为5的概率是| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
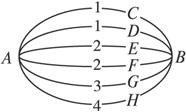
(1)设选取的三条网线由A到B可通过的信息总量为x,当x≥6时,才能保证信息畅通,求线路信息畅通的概率.
(2)求选取的三条网线可通过信息总量的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com