
【题目】如图,已知△![]() 中,∠
中,∠![]() =90°,
=90°,![]() ,且
,且![]() =1,
=1,![]() =2,△
=2,△![]() 绕
绕![]() 旋转至
旋转至![]() ,使点
,使点![]() 与点
与点![]() 之间的距离
之间的距离![]() =
=![]() .
.
(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求异面直线![]() 与
与![]() 所成的角的余弦值.
所成的角的余弦值.

【答案】(1)见详解;(2)60°;(3)![]() .
.
【解析】
(1)∵CD⊥AB,∴CD⊥A′D,CD⊥DB,∴CD⊥平面A′BD,
∴CD⊥BA′.又在△A′DB中,A′D=1,DB=2,A′B=![]()
,∴∠BA′D=90°,
即BA′⊥A′D,∴BA′⊥平面A′CD.
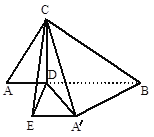
(2)∵CD⊥DB,CD⊥A′D,∴∠BDA′是二面角
A′—CD—B的平面角.又Rt△A′BD中,A′D=1,BD=2,
∴∠A′DB=60°,即 二面角A′—CD—B为60°.
(3)过A′作A′E∥BD,在平面A′BD中作DE⊥A′E于E,
连CE,则∠CA′E为A′C与BD所成角.
∵CD⊥平面A′BD,DE⊥A′E,∴A′E⊥CE.
∵EA′∥AB,∠A′DB=60°,∴∠DA′E=60°,又A′D=1,∠DEA′=90°,∴A′E=![]()
又∵在Rt△ACB中,AC=![]() =
=![]() ∴A′C=AC=
∴A′C=AC=![]()
∴cos∠CA′E=![]() =
=![]() =
=![]() ,即A′C与BD所成角的余弦值为
,即A′C与BD所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与x轴交点为
的图象与x轴交点为![]() ,与此交点距离最小的最高点坐标为
,与此交点距离最小的最高点坐标为![]() .
.
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)若函数![]() 满足方程
满足方程![]() ,求方程在
,求方程在![]() 内的所有实数根之和;
内的所有实数根之和;
(Ⅲ)把函数![]() 的图像的周期扩大为原来的两倍,然后向右平移
的图像的周期扩大为原来的两倍,然后向右平移![]() 个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数
个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数![]() 的图像.若对任意的
的图像.若对任意的![]() ,方程
,方程![]() 在区间
在区间![]() 上至多有一个解,求正数k的取值范围.
上至多有一个解,求正数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),且满足
),且满足![]() .
.
(1)求a的值;
(2)设函数![]() ,
,![]() (
(![]() ),若存在
),若存在![]() ,
,![]() ,使得
,使得![]() 成立,求实数t的取值范围;
成立,求实数t的取值范围;
(3)若存在实数m,使得关于x的方程![]() 恰有4个不同的正根,求实数m的取值范围.
恰有4个不同的正根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系![]() 的坐标平面
的坐标平面![]() 内,若函数
内,若函数 的图象与
的图象与![]() 轴围成一个封闭区域
轴围成一个封闭区域![]() ,将区域
,将区域![]() 沿
沿![]() 轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向上移4个单位,得到几何体如图一.现有一个与之等高的圆柱如图二,其底面积与区域![]() 面积相等,则此圆柱的体积为__________.
面积相等,则此圆柱的体积为__________.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图象如图所示,点A,B,C在图象
的部分图象如图所示,点A,B,C在图象![]() 上,
上,![]() ,
,![]() ,并且
,并且![]() 轴
轴
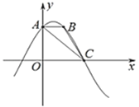
(1)求![]() 和
和![]() 的值及点B的坐标;
的值及点B的坐标;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)将函数![]() 的图象上各点的纵坐标变为原来的
的图象上各点的纵坐标变为原来的![]() 倍,横坐标不变,再将所得图象各点的横坐标变为原来的
倍,横坐标不变,再将所得图象各点的横坐标变为原来的![]() 倍,纵坐标不变,最后将所得图象向右平移
倍,纵坐标不变,最后将所得图象向右平移![]() 个单位,得到
个单位,得到![]() 的图象,若关于x的方程
的图象,若关于x的方程![]() 在区间
在区间![]() 上有两个不同解,求实数a的取值范围.
上有两个不同解,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com