
如图,在三棱锥中S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.

求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源:2014年高考数学(理)二轮专题复习真题感悟1-6练习卷(解析版) 题型:选择题
设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为 ( ).
A.y=x-1或y=-x+1
B.y= (x-1)或y=-
(x-1)或y=-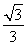 (x-1)
(x-1)
C.y= (x-1)或y=-
(x-1)或y=- (x-1)
(x-1)
D.y= (x-1)或y=-
(x-1)或y=- (x-1)
(x-1)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习真题感悟1-2练习卷(解析版) 题型:选择题
已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则 ( ).
A.a>0,4a+b=0 B.a<0,4a+b=0
C.a>0,2a+b=0 D.a<0,2a+b=0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题4练习卷(解析版) 题型:解答题
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.

(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题3练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,若双曲线 -
- =1的离心率为
=1的离心率为 ,则m的值为________.
,则m的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题2练习卷(解析版) 题型:填空题
设1=a1≤a2≤…≤a7,其中a1,a3,a5,a7成公比为q的等比数列,a2,a4,a6成公差为1的等差数列,则q的最小值是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题1练习卷(解析版) 题型:填空题
若曲线y=kx+ln x在点(1,k)处的切线平行于x轴,则k=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测4练习卷(解析版) 题型:填空题
设圆x2+y2=2的切线l与x轴正半轴、y轴正半轴分别交于点A,B,当|AB|取最小值时,切线l的方程为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com