解:(1)由

得

,
则

,任取

,
都有f(-x)=

=-f(x),则该函数为奇函数.
(2)任取0<x
1<x
2<1,
则有0<x
12<x
22<1?2-x
12>2-x
22>1,?ln(2-x
12)>ln(2-x
22)>0.
又

,
所以

,
即f(x
1)>f(x
2),
故函数f(x)在区间(0,1)上单调递减.
(3)由程序框图知,公差不为零的等差数列{a
n}要满足条件,
则必有f(a
1)+f(a
2)+…+f(a
10)=0.
由(1)知函数f(x)是奇函数,而奇函数的图象关于原点对称,
所以要构造满足条件的等差数列{a
n},可利用等差数列的性质,只需等差数列{a
n}
满足:a
1+a
10=a
2+a
9═a
5+a
6=0
且

即可.
我们可以先确定a
5,a
6使得a
5+a
6=0,因为公差不为零的等差数列{a
n}必是单调的数列,只要它的最大项和最小项在

中,即可满足要求.
所以只要a
5,a
6对应的点尽可能的接近原点.如取a
5=-0.1,a
6=0.1,存在满足条件的一个等差数列{a
n}可以是a
n=0.2n-1.1(1≤n≤10,n∈N
*).
(文科)(1)由题意,不难发现A、C两点分别在x轴正负半轴上.设两点坐标分别为A(a,0),C(c,0),
则有ac<0.
对于圆方程x
2+y
2+Dx+Ey+F=0,
当y=0时,可得x
2+Dx+F=0,其中方程的两根分别为点A和点C的横坐标,于是有x
Ax
C=ac=F.
因为ac<0,故F<0.
(2)对角线互相垂直的四边形ABCD面积
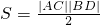
,
因为S=8,|AC|=2,可得|BD|=8.
又因为
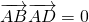
,
所以∠A为直角,而因为四边形是圆M的内接四边形,
故|BD|=2r=8?r=4.
对于方程x
2+y
2+Dx+Ey+F=0所表示的圆,
可知
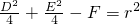
,
所以D
2+E
2-4F=4r
2=64.
(3)证:设四边形四个顶点的坐标分别为A(a,0),B(0,b),C(c,0),D(0,d).
则可得点G的坐标为
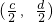
,即
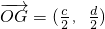
.
又
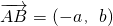
,且AB⊥OH,故要使G、O、H三点共线,只需证
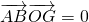
即可.
而
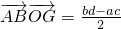
,且对于圆M的一般方程x
2+y
2+Dx+Ey+F=0,
当y=0时可得x
2+Dx+F=0,其中方程的两根分别为点A和点C的横坐标,
于是有x
Ax
C=ac=F.
同理,当x=0时,可得y
2+Ey+F=0,其中方程的两根分别为点B和点D的纵坐标,
于是有y
By
D=bd=F.
所以,
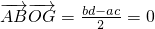
,即AB⊥OG.
故O、G、H必定三点共线.
分析:理科(1)先求出函数的定义域,得到定义域关于原点对称,在检验-x与x的函数值之间的关系,得到奇函数.
(2)根据单调性的定义,设出已知大小关系的任意两个变量,利用定义证明函数的单调性,得到函数是一个增函数.
(3)由程序框图知,公差不为零的等差数列{a
n}要满足条件,则必有f(a
1)+f(a
2)+…+f(a
10)=0.所以要构造满足条件的等差数列{a
n},可利用等差数列的性质,只需等差数列{a
n}满足:a
1+a
10=a
2+a
9═a
5+a
6=0.
文科(1)发现A、C两点分别在x轴正负半轴上.设两点坐标分别为A(a,0),C(c,0),则有ac<0.对于圆方程x
2+y
2+Dx+Ey+F=0,当y=0时,可得x
2+Dx+F=0,其中方程的两根分别为点A和点C的横坐标,于是有x
Ax
C=ac=F,得到故F<0.
(2)写出对角线互相垂直的四边形ABCD面积,根据两个向量的数量积等于0,整理出角是一个直角,根据圆的方程写出结果.
(3)设出和写出要用的点的坐标,当y=0时可得x
2+Dx+F=0,其中方程的两根分别为点A和点C的横坐标,于是有x
Ax
C=ac=F.同理,当x=0时,可得y
2+Ey+F=0,其中方程的两根分别为点B和点D的纵坐标,于是有y
By
D=bd=F.得到结果.
点评:本题是一个文理合卷的题目,有两个题目分别考查函数的性质和直线与圆的方程,本题解题的关键是看清题目的实质,抓住解题的主要方法.


 (理)已知函数
(理)已知函数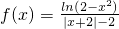 .
.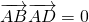 ,求D2+E2-4F的值;
,求D2+E2-4F的值;
 ,
, ,任取
,任取 ,
, =-f(x),则该函数为奇函数.
=-f(x),则该函数为奇函数. ,
, ,
, 即可.
即可. 中,即可满足要求.
中,即可满足要求.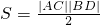 ,
,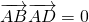 ,
,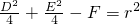 ,
,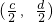 ,即
,即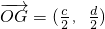 .
.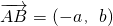 ,且AB⊥OH,故要使G、O、H三点共线,只需证
,且AB⊥OH,故要使G、O、H三点共线,只需证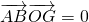 即可.
即可.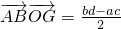 ,且对于圆M的一般方程x2+y2+Dx+Ey+F=0,
,且对于圆M的一般方程x2+y2+Dx+Ey+F=0,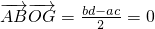 ,即AB⊥OG.
,即AB⊥OG.

 阅读快车系列答案
阅读快车系列答案 ,其中
,其中 .
. ,使得
,使得 成立,求实数
成立,求实数 的取值范围;
的取值范围; 的值域.
的值域.