Question

定义在R上的奇函数f（x）满足当x＞0时f（x）=x²-2x+2．
（1）求f（f（-1））的值
（2）求f（x）的解析式
（3）在所给坐标系中画出f（x）的图象，写出单调区间．

Answer 1

解：（1）因为f（x）为奇函数，
所以f（-1）=-f（1）=-（1-2+2）=-1，
所以f（f（-1））=f（-1）=-1；
（2）由奇函数性质可得，f（-0）=-f（0），解得f（0）=0；
当x＜0时，-x＞0，则f（-x）=（-x）²-2（-x）+2=x²+2x+2，
所以f（x）=-f（-x）=-x²-2x-2；
所以f（x）=；
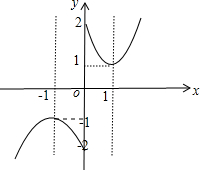
（3）由（2）作出f（x）的图象如右所示：
根据图象可得增区间为：（-∞，-1）和（（1，+∞）；减区间为：（-1，0）和（0，1）．
分析：（1）易求f（1），所以f（-1）=-f（1），进而可求得f（f（-1））的值；
（2）只需求x≤0时f（x）表达式，由f（-0）=-f（0）可得f（0），x＜0时，先求f（-x），根据f（x）与f（-x）关系可得f（x）；
（3）由（2）可作出f（x）草图，根据图象可得其单调区间；
点评：本题考查函数的奇偶性及其应用，属基础题．