
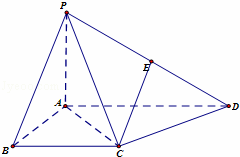
如图,四棱锥P﹣ABCD中,PA⊥面ABCD.底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=AB=BC=![]() AD=1.E为PD的中点.
AD=1.E为PD的中点.
(1)求证:CE∥平面PAB;
(2)求异面直线AB与PC所成的角的正切值.
考点:
异面直线及其所成的角;直线与平面平行的判定.
专题:
计算题;空间角.
分析:
(1)取AD的中点F.连接EF,CF.由题设条件推导出EF∥PA,CF∥AB,得到面EFC∥面PAB,由此能够证明CE∥面PAB.
(2)由CF∥AB,知∠PCF为异面直线AB与PC所成的角,利用题设条件推导出CF⊥面PAD,由此能够求出异面直线AB与PC所成的角的正切值.
解答:
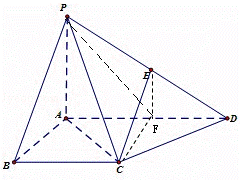
解:(1)取AD的中点F.连接EF,CF.
∵PA⊥面ABCD.底面ABCD为直角梯形,∠ABC=∠BAD=90°,BC=![]() AD,E为PD的中点.
AD,E为PD的中点.
∴EF∥PA,CF∥AB,
∴面EFC∥面PAB,
所以CE∥面PAB.…(6分)
(2)∵CF∥AB,
∴∠PCF为异面直线AB与PC所成的角,
∵∠BAD=90°,CF∥AB,∴CF⊥AD,
∵PA⊥面ABCD,CF⊂平面ABCD,∴CF⊥PA,
又∵PA∩AD=A,∴CF⊥面PAD.
∵PA=AB=BC=![]() AD=1,
AD=1,
∴PF=![]() ,CF=1,
,CF=1,
∴在直角△PCF中,
tan∠PCF=![]() =
=![]() .
.
故异面直线AB与PC所成的角的正切值为![]() .…(12分)
.…(12分)
点评:
本题考查直线与平面平行的证明,考查异面直线所成角的正切值的求法,解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.


科目:高中数学 来源: 题型:
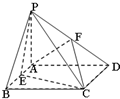 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E,F分别是AB,PD的中点,若PA=AD=3,CD=
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E,F分别是AB,PD的中点,若PA=AD=3,CD=| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
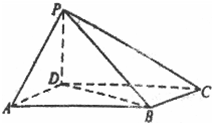 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•安徽)如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
(2013•安徽)如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E、F分别是AB、PD的中点.若PA=AD=3,CD=
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E、F分别是AB、PD的中点.若PA=AD=3,CD=| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,且PA=4,AD=6,F,E分别是线段PD,CD的中点.
如图,四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,且PA=4,AD=6,F,E分别是线段PD,CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com