设函数 f (x)=ax-lnx-3(a∈R),g(x)=xe1-x.
(Ⅰ)若函数g(x)的图象在点(0,0)处的切线也恰为f(x)图象的一条切线,求实数a的值;
(Ⅱ)是否存在实数a,对任意的x∈(0,e],都有唯一的x∈[e-4,e],使得f(x)=g(x)成立.若存在,求出a的取值范围;若不存在,请说明理由.
【答案】
分析:(Ⅰ)先求g(x)的图象在(0,0)处的切线方程是y=ex,再利用函数g(x)的图象在点(0,0)处的切线也恰为f(x)图象的一条切线,可求a的值;
(Ⅱ)先确定函数g(x)的值域,令m=g(x),则原命题等价于对于任意m∈(0,1],都有唯一的
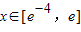
,使得f(x
)=m成立,而
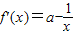
,x∈[e
-4,e],
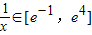
,分类讨论,确定函数的单调性,求函数的最值,即可求得结论.
解答:解:(Ⅰ)∵g'(x)=(1-x)e
1-x,∴g'(0)=e,∴g(x)的图象在(0,0)处的切线方程是y=ex;(2分)
设y=ex与f(x)的图象切于点(x
,y
),而
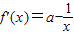
,∴
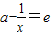
且ax
-lnx
-3=ex
,解得a=e
2+e; (5分)
(Ⅱ)∵g'(x)=(1-x)e
1-x,∴g(x)在(0,1]上单调递增,在[1,e]上单调递减,
且g(0)=0,g(1)=1,g(e)=e
2-e∈(0,1),∴g(x)∈(0,1]; (8分)
若令m=g(x),则原命题等价于对于任意m∈(0,1],都有唯一的
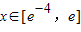
,使得f(x
)=m成立. (9分)
而
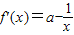
,x∈[e
-4,e],
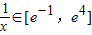
①当a≤0时,f'(x)<0恒成立,所以f(x)在x∈[e
-4,e]上单调递减,要满足条件,则必须有
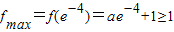
,且f
min=f(e)=ae-4≤0,无解,所以此时不存在满足条件的a;(10分)
②当0<a≤e
-1,f'(x)<0恒成立,所以f(x)在x∈[e
-4,e]上单调递减,要满足条件,则必须有
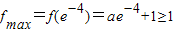
,且f
min=f(e)=ae-4≤0,解得
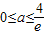
,∴0<a≤e
-1;(11分)
③当e
-1<a<e
4时,f(x)在区间
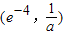
上单调递减,在
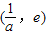
上单调递增,
又f(e
-4)=ae
-4+1>1,要满足条件,则
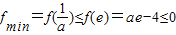
,解得
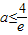
,∴
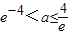
;(12分)
④当a≥e
4时,f'(x)>0恒成立,所以f(x)在x∈[e
-4,e]上单调递增,
又
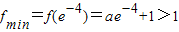
,所以此时不存在a满足条件; (13分)
综上有
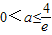
. (15分)
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,考查分类讨论的数学思想,属于中档题.

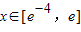 ,使得f(x)=m成立,而
,使得f(x)=m成立,而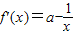 ,x∈[e-4,e],
,x∈[e-4,e],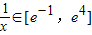 ,分类讨论,确定函数的单调性,求函数的最值,即可求得结论.
,分类讨论,确定函数的单调性,求函数的最值,即可求得结论.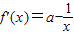 ,∴
,∴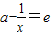 且ax-lnx-3=ex,解得a=e2+e; (5分)
且ax-lnx-3=ex,解得a=e2+e; (5分)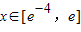 ,使得f(x)=m成立. (9分)
,使得f(x)=m成立. (9分)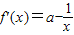 ,x∈[e-4,e],
,x∈[e-4,e],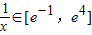
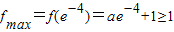 ,且fmin=f(e)=ae-4≤0,无解,所以此时不存在满足条件的a;(10分)
,且fmin=f(e)=ae-4≤0,无解,所以此时不存在满足条件的a;(10分)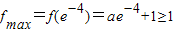 ,且fmin=f(e)=ae-4≤0,解得
,且fmin=f(e)=ae-4≤0,解得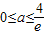 ,∴0<a≤e-1;(11分)
,∴0<a≤e-1;(11分)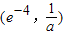 上单调递减,在
上单调递减,在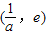 上单调递增,
上单调递增,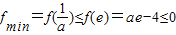 ,解得
,解得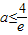 ,∴
,∴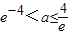 ;(12分)
;(12分)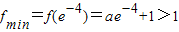 ,所以此时不存在a满足条件; (13分)
,所以此时不存在a满足条件; (13分)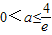 . (15分)
. (15分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案