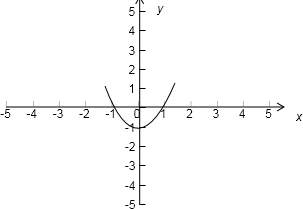f(x)=2x2-1的单调区间及单调性.→变题:f(x)=|2x2-1|的单调区间.
解:由f(x)=2x
2-1,画出图形为:
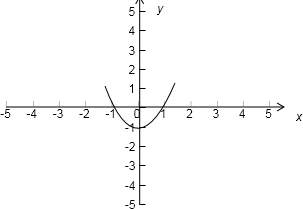
由所画的图形可以知道:此函数的单调递增区间为(0,+∞),函数在(0,+∞)上单调递增;
此函数的单调递减区间为:(-∞,0),函数在(-∞,0)上单调递减.
对于变式:f(x)=|2x
2-1|的图形为当2x
2-1≥0即x∈[1,+∞)或x∈(-∞,-1]时保持原抛物线在x轴上方的不变,
把原抛物线在x轴下方即2x
2-1<0即x∈(-1,1)时的图形关于x轴对称过来,从新组成的图形即为f(x)=|2x
2-1|的图象,所以此函数的单调递增区间为:
(-1,0),(1,+∞);单调递减区间为:(0,1),(-∞,-1).
分析:由题意f(x)=2x
2-1,为具体的二次函数,利用二次函数的图形及基本性质即可;对于变题,可以整个解析式带绝对值可以利用图形变换得.
点评:此题考查了二次函数的图形及二次函数的基本的单调性,还考查了对于整个解析式加一绝对值时的图形变换.