
(本小题满分12分) 一个黑色小布袋,袋中有 只黄色、
只黄色、 只红色的乒乓球(除颜色外其体积、质地完全相同),从袋中随机摸出
只红色的乒乓球(除颜色外其体积、质地完全相同),从袋中随机摸出 个球,
个球,
(1)求摸出的 个球为红球和摸出的
个球为红球和摸出的 个至少一球为黄球的概率分别是多少?
个至少一球为黄球的概率分别是多少?
(2)求摸出的 个球的颜色不相同的概率是多少?
个球的颜色不相同的概率是多少?
(1) ,
,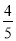 ;(2)
;(2)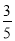 .
.
【解析】
试题分析:(1)先用列举法写出从装有 只黄色、
只黄色、 只红色的乒乓球的袋子中任取
只红色的乒乓球的袋子中任取 个球所有的基本事件的个数,设“从袋中随机摸出
个球所有的基本事件的个数,设“从袋中随机摸出 个球是红球”为事件
个球是红球”为事件 ,判断“摸出的
,判断“摸出的 个至少一个球是黄球”为事件
个至少一个球是黄球”为事件 的对立事件
的对立事件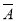 ,求出事件
,求出事件 包含的基本事件的个数,再用古典概型的概率计算公式求出
包含的基本事件的个数,再用古典概型的概率计算公式求出 ,用对立事件的概率计算公式求出
,用对立事件的概率计算公式求出 ;(2)设“摸出的
;(2)设“摸出的 个球的颜色不相同”为事件
个球的颜色不相同”为事件 ,求出事件
,求出事件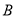 包含的基本事件的个数,再用古典概型的概率计算公式求出
包含的基本事件的个数,再用古典概型的概率计算公式求出 ;对于求概率问题,首先要判断题目涉及的事件的概率类型,选用恰当的概率公式进行计算,其次在求出概率后,要对题中问题进行回答.
;对于求概率问题,首先要判断题目涉及的事件的概率类型,选用恰当的概率公式进行计算,其次在求出概率后,要对题中问题进行回答.
试题解析:(1)袋中的 只黄色的乒乓球分别记作为
只黄色的乒乓球分别记作为 、
、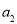 、
、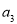 ,
,  只红色的乒乓球分别记作为
只红色的乒乓球分别记作为 、
、 、
、 ,从袋中随机摸出
,从袋中随机摸出 个球所有的基本事件的个数为
个球所有的基本事件的个数为 个,它们分别为:
个,它们分别为: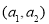 、
、 、
、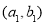 、
、 、
、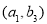 、
、 、
、 、
、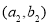 、
、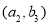 、
、 、
、 、
、 、
、 、
、 、
、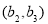 ; 2分
; 2分
设“从袋中随机摸出 个球是红球”为事件
个球是红球”为事件 ,则“摸出的
,则“摸出的 个至少一个球是黄球”为事件
个至少一个球是黄球”为事件 的对立事件,记作
的对立事件,记作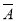 ,且事件
,且事件 包含
包含 个基本事件,它们分别为:
个基本事件,它们分别为: 、
、 、
、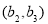 ; 3分
; 3分
由古典概型概率计算公式可知,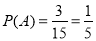 , 4分
, 4分
由对立事件的概率计算公式得, . 5分
. 5分
所以从袋中随机摸出 个球,摸出的
个球,摸出的 个球为红色的概率是
个球为红色的概率是 ,摸出的
,摸出的 个至少一球是黄球的概率为
个至少一球是黄球的概率为 . 6分
. 6分
(2) 设“摸出的 个球的颜色不相同”为事件
个球的颜色不相同”为事件 ,则事件
,则事件 包含9个基本事件,它们分别为:
包含9个基本事件,它们分别为: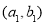 、
、 、
、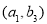 、
、 、
、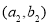 、
、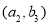 、
、 、
、 、
、 ; 8分
; 8分
由古典概型计算公式可知, . 10分
. 10分
所以从袋中随机摸出 个球,摸出的
个球,摸出的 个球的颜色不相同的概率是
个球的颜色不相同的概率是 . 12分
. 12分
考点:①古典概型的概率计算;②对立事件的概率计算.


科目:高中数学 来源:2014-2015学年安徽省高二10月月考理科数学试卷(解析版) 题型:选择题
下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是( )
游戏 | 游戏 | 游戏 |
|
|
|
取 | 取 | 取 |
取出的两个球同色→甲胜 | 取出的球是黑球→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 |
A.游戏 和游戏
和游戏 B.游戏
B.游戏 C.游戏
C.游戏 D.游戏
D.游戏
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省高二10月月考文科数学试卷(解析版) 题型:填空题
给出下列结论:
①命题“ ”的否定是“
”的否定是“ ”;
”;
②命题“有些正方形是平行四边形”的否定是“所有正方形不都是平行四边形”;
③命题“ 是对立事件”是命题“
是对立事件”是命题“ 是互斥事件”的充分不必要条件;
是互斥事件”的充分不必要条件;
④若 ,
,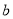 是实数,则“
是实数,则“ 且
且 ”是“
”是“ 且
且 ”的必要不充分条件.
”的必要不充分条件.
其中正确结论的是 _________________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省高二10月月考文科数学试卷(解析版) 题型:选择题
设命题甲:|x-2|<3,命题乙: ,那么甲是乙的( )
,那么甲是乙的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com