
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,下顶点为
,下顶点为![]() ,
,![]() 为椭圆的左、右焦点,过右焦点的直线与椭圆交于
为椭圆的左、右焦点,过右焦点的直线与椭圆交于![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)经过点![]() 的直线与椭圆
的直线与椭圆![]() 交于不同的两点
交于不同的两点![]() (均异于点
(均异于点![]() ),试探求直线
),试探求直线![]() 与
与![]() 的斜率之和是否为定值,证明你的结论.
的斜率之和是否为定值,证明你的结论.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量。![]() 年,某企业连续
年,某企业连续![]() 年累计研发投入搭
年累计研发投入搭![]() 亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这
亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这![]() 年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
年间的研发投入(单位:十亿元)用右图中的折现图表示,根据折线图和条形图,下列结论错误的使( )
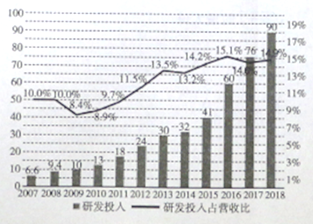
A. ![]() 年至
年至![]() 年研发投入占营收比增量相比
年研发投入占营收比增量相比![]() 年至
年至![]() 年增量大
年增量大
B. ![]() 年至
年至![]() 年研发投入增量相比
年研发投入增量相比![]() 年至
年至![]() 年增量小
年增量小
C. 该企业连续![]() 年研发投入逐年增加
年研发投入逐年增加
D. 该企业来连续![]() 年来研发投入占营收比逐年增加
年来研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
(1)在频率分布直方图中,中位数左边和右边的直方图的面积相等.
(2)如果一组数中每个数减去同一个非零常数,则这一组数的平均数改变,方差不改变.
(3)一个样本的方差s2=![]() [(x
[(x![]() 一3)2+(X
一3)2+(X![]() —3)2+ +(X
—3)2+ +(X![]() 一3)2],则这组数据总和等于60.
一3)2],则这组数据总和等于60.
(4)数据![]() 的方差为
的方差为![]() ,则数据
,则数据![]() 的方差为
的方差为![]() .
.
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友某日在某淘宝店的网购情况,随机抽查了该市当天![]() 名网友的网购金额情况,得到如下统计表(如图).
名网友的网购金额情况,得到如下统计表(如图).
网购金额(单位:千元) | 频数 | 频率 |
| 3 | 0.05 |
|
|
|
| 9 | 0.15 |
| 15 | 0.25 |
| 18 | 0.30 |
|
|
|

若网购金额超过![]() 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过![]() 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为![]() .
.
(Ⅰ)试确定![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(Ⅱ)该营销部门为了进一步了解这![]() 名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取
名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取![]() 人,若需从这
人,若需从这![]() 人中随机选取
人中随机选取![]() 人进行问卷调查.设
人进行问卷调查.设![]() 为选取的
为选取的![]() 人中“网购达人”的人数,求
人中“网购达人”的人数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与平面
与平面![]() 相交但不垂直,则下列说法中正确的是( )
相交但不垂直,则下列说法中正确的是( )
A.在平面![]() 内没有直线与直线
内没有直线与直线![]() 垂直;
垂直;
B.在平面![]() 内有且只有一条直线与直线
内有且只有一条直线与直线![]() 垂直;
垂直;
C.在平面![]() 内有无数条直线与直线
内有无数条直线与直线![]() 垂直;
垂直;
D.在平面![]() 内存在两条相交直线与直线
内存在两条相交直线与直线![]() 垂直.
垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
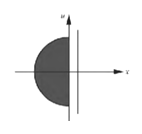
【题目】关于旋转体的体积,有如下的古尔丁(guldin)定理:“平面上一区域D绕区域外一直线(区域D的每个点在直线的同侧,含直线上)旋转一周所得的旋转体的体积,等于D的面积与D的几何中心(也称为重心)所经过的路程的乘积”.利用这一定理,可求得半圆盘 ,绕直线x
,绕直线x![]() 旋转一周所形成的空间图形的体积为_____.
旋转一周所形成的空间图形的体积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,边
中,边![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,![]() ,过
,过![]() 边上一点
边上一点![]() (异于端点)引边
(异于端点)引边![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,再由
,再由![]() 引边
引边![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,又由
,又由![]() 引边
引边![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,同样的操作连续进行,得到点列
,同样的操作连续进行,得到点列![]() 、
、![]() 、
、![]() ,设
,设![]() (
(![]() );
);
(1)求![]() ;
;
(2)结论“![]() ”是否正确?请说明理由;
”是否正确?请说明理由;
(3)若对于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com