
分析 设出z=a+bi(a,b∈R),代入z+|z|,然后列出方程组,求解即可得a,b的值,再由复数求模公式即可得答案.
解答 解:设z=a+bi(a,b∈R),
则z+|z|=a+bi+$\sqrt{{a}^{2}+{b}^{2}}$=2+8i,
∴$\left\{\begin{array}{l}{a+\sqrt{{a}^{2}+{b}^{2}}=2}\\{b=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-15}\\{b=8}\end{array}\right.$.
则|z|=$\sqrt{(-15)^{2}+{8}^{2}}=17$.
故答案为:17.
点评 本题考查了复数求模,考查了复数相等的基本条件,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | -2<k<4 | B. | $-\frac{1}{2}<k<4$ | C. | -2<k≤1 | D. | $-\frac{1}{2}<k≤1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
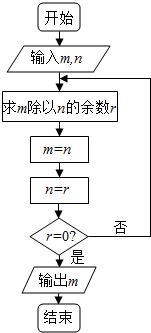 如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )
如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法,执行改程序框图,若输入的m,n的值分别为30,42,则输出的m=( )| A. | 0 | B. | 2 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$或0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{π}{6}})$ | B. | $({\frac{π}{6},\frac{π}{4}})$ | C. | $({\frac{π}{4},\frac{π}{3}})$ | D. | $({\frac{π}{3},\frac{π}{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com