
设向量
(1)若 ,求
,求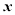 的值
的值
(2)设函数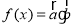 ,求
,求 的取值范围
的取值范围
(1)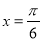 ;(2)
;(2)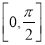 .
.
【解析】
试题分析: (1)利用向量的模长公式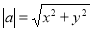 化简得到关于
化简得到关于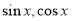 关系式,进而求得
关系式,进而求得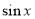 的值,再利用三角函数值,结合角的范围求得
的值,再利用三角函数值,结合角的范围求得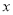 的值;(2)利用三角恒等变形化成
的值;(2)利用三角恒等变形化成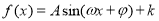 ,再利用三角函数的图像与性质求解.规律总结:1.涉及平面向量的模长、数量积等运算时,要合理选用公式(向量形式或坐标形式); 2.三角恒等变形的关键,要正确运用公式及其变形,如:二倍角公式的变形
,再利用三角函数的图像与性质求解.规律总结:1.涉及平面向量的模长、数量积等运算时,要合理选用公式(向量形式或坐标形式); 2.三角恒等变形的关键,要正确运用公式及其变形,如:二倍角公式的变形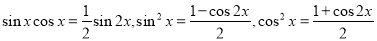 ,
,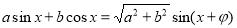
求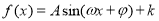 在某区间的值域时,一定要结合正弦函数、余弦函数的图像求解.
在某区间的值域时,一定要结合正弦函数、余弦函数的图像求解.
注意点:学生对公式及其变形运用的灵活性不够,学生应加强公式的记忆和应用;求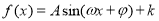 的值域时,学生不善于利用数形结合思想,往往想当然,最大值为1,最小值为-1.
的值域时,学生不善于利用数形结合思想,往往想当然,最大值为1,最小值为-1.
试题解析:(1)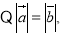
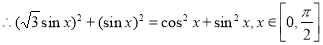
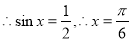
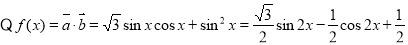
=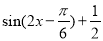 又
又 ;
;
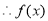 的取值范围是
的取值范围是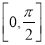 .
.
考点:1.平面向量的数量积,2.三角恒等变形,3.三角函数的图像与性质


科目:高中数学 来源:2016届甘肃省高一下学期期中考试数学试卷(解析版) 题型:选择题
用系统抽样法从160名学生中抽取容量为20的样本,将160名学生随机地从1~160编号,按编号顺序平均分成20组(1~8号,9~16号,…,153~160号),若第16组抽出的号码为126,则第1组中用抽签的方法确定的号码是( )
(A)5 (B)6 (C)7 (D)8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com