
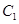 的参数方程是
的参数方程是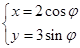 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线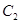 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在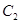 上,且A,B,C,D依逆时针次序排列,点A的极坐标为
上,且A,B,C,D依逆时针次序排列,点A的极坐标为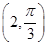 .
. 上任意一点,求
上任意一点,求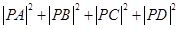 的取值范围.
的取值范围. ),B(-
),B(- ,1),C(-1,-
,1),C(-1,- ),D(
),D( ,-1);(Ⅱ)
,-1);(Ⅱ)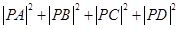 的取值范围是[32,52]
的取值范围是[32,52]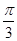 ,2sin
,2sin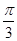 ),B(2cos(
),B(2cos(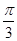 +
+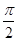 ),2sin(
),2sin(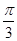 +
+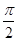 )),C(2cos(
)),C(2cos(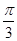 +π),2sin(
+π),2sin(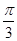 +π)),D(2cos(
+π)),D(2cos(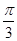 +
+ ),2sin(
),2sin(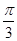 +
+ )),然后将其化为直角坐标即可;(Ⅱ)设P(2cosφ,3sinφ),令S=
)),然后将其化为直角坐标即可;(Ⅱ)设P(2cosφ,3sinφ),令S=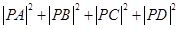 ,利用三角函数求解.
,利用三角函数求解.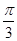 ,2sin
,2sin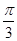 ),B(2cos(
),B(2cos(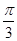 +
+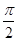 ),2sin(
),2sin(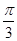 +
+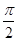 )),
)),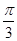 +π),2sin(
+π),2sin(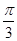 +π)),D(2cos(
+π)),D(2cos(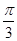 +
+ ),2sin(
),2sin(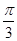 +
+ )),4分
)),4分 ),B(-
),B(- ,1),C(-1,-
,1),C(-1,- ),D(
),D( ,-1). 5分
,-1). 5分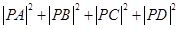 ,
,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com