
【题目】如图,点![]() 是正方体
是正方体![]() 中的侧面
中的侧面![]() 上的一个动点,则下列结论正确的是( )
上的一个动点,则下列结论正确的是( )
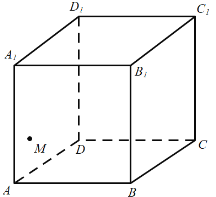
A.点![]() 存在无数个位置满足
存在无数个位置满足![]()
B.若正方体的棱长为1,三棱锥![]() 的体积最大值为
的体积最大值为![]()
C.在线段![]() 上存在点
上存在点![]() ,使异面直线
,使异面直线![]() 与
与![]() 所成的角是
所成的角是![]()
D.点![]() 存在无数个位置满足到直线
存在无数个位置满足到直线![]() 和直线
和直线![]() 的距离相等.
的距离相等.
【答案】ABD
【解析】
通过证明![]() 面
面![]() ,可得当点
,可得当点![]() 上时,有
上时,有![]() ,可判断A;由已知
,可判断A;由已知![]() ,当点
,当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 到面
到面![]() 的距离最大,计算
的距离最大,计算![]() 可判断B;C. 连接
可判断B;C. 连接![]() ,因为
,因为![]() ,则
,则![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角,利用余弦定理算出
所成的角,利用余弦定理算出![]() 的距离,可判断C;连接
的距离,可判断C;连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,得到
,得到![]() ,则点
,则点![]() 在以
在以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线上,可判断D.
为准线的抛物线上,可判断D.
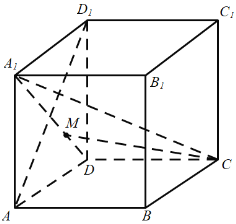
解:A.连接![]() ,
,
由正方体的性质可得![]() ,
,
则![]() 面
面![]()
当点![]() 上时,有
上时,有![]() ,
,
故点![]() 存在无数个位置满足
存在无数个位置满足![]() ,
,
故A正确;
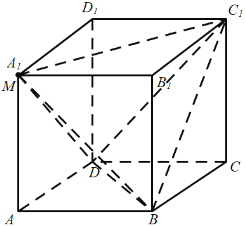
B.由已知![]() ,
,
当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 到面
到面![]() 的距离最大,
的距离最大,
则三棱锥![]() 的体积最大值为
的体积最大值为![]() ,
,
故B正确;
C. 连接![]() ,因为
,因为![]()
则![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角
所成的角
设正方体棱长为1,![]() ,则
,则![]() ,
,
点![]() 到线
到线![]() 的距离为
的距离为![]() ,
,![]()
![]() ,
,
解得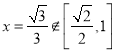 ,
,
所以在线段![]() 上不存在点
上不存在点![]() ,使异面直线
,使异面直线![]() 与
与![]() 所成的角是
所成的角是![]() ,
,
故C错误;
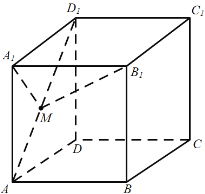
D. 连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
由![]() 面
面![]() ,
,![]() 面
面![]() ,得
,得![]() ,
,
则![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,
由已知![]() ,
,
则点![]() 在以
在以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线上,故这样的点
为准线的抛物线上,故这样的点![]() 有无数个,
有无数个,
故D正确.
故选:ABD.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】现有一排10个位置的空停车场,甲、乙、丙三辆不同的车去停放,要求每辆车左右两边都有空车位且甲车在乙、丙两车之间的停放方式共有_________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实数k,b,使得函数![]() 和
和![]() 对其定义域上的任意实数x同时满足:
对其定义域上的任意实数x同时满足:![]() 且
且![]() ,则称直线:
,则称直线:![]() 为函数
为函数![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() (其中e为自然对数的底数).试问:
(其中e为自然对数的底数).试问:
(1)函数![]() 和
和![]() 的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
(2)函数![]() 和
和![]() 是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了A,B两种小区管理方案,为了决定选取哪种方案为小区的最终管理方案,随机选取了4名物业人员进行投票,物业人员投票的规则如下:①单独投给A方案,则A方案得1分,B方案得﹣1分;②单独投给B方案,则B方案得1分,A方案得﹣1分;③弃权或同时投票给A,B方案,则两种方案均得0分.前1名物业人员的投票结束,再安排下1名物业人员投票,当其中一种方案比另一种方案多4分或4名物业人员均已投票时,就停止投票,最后选取得分多的方案为小区的最终管理方案.假设A,B两种方案获得每1名物业人员投票的概率分别为![]() 和
和![]() .
.
(1)在第1名物业人员投票结束后,A方案的得分记为ξ,求ξ的分布列;
(2)求最终选取A方案为小区管理方案的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 | 17 | 41 | 62 | 50 | 26 | 3 | 1 |
(1)求这200名患者的潜伏期的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述200名患者中抽取40人得到如下列联表.请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
50岁以上(含50岁) | 20 | ||
50岁以下 | 9 | ||
总计 | 40 |
(3)以这200名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入硏究,该研究团队在该地区随机调查了10名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
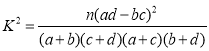 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,
(x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,![]() ).
).
(Ⅰ)若f(x)≥0在x∈R上恒成立,求实数a的取值范围;
(Ⅱ)若ex≥lnx+m对任意x>0恒成立,求证:实数m的最大值大于2.3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与直线
与直线![]() 分别与椭圆
分别与椭圆![]()
![]() 交于点
交于点![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,是否存在经过原点,且以
两点,是否存在经过原点,且以![]() 为直径的圆?若有,请求出圆的方程,若没有,请说明理由.
为直径的圆?若有,请求出圆的方程,若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期的数学家祖暅提出了计算几何体体积的祖暅原理:“幂势既同,则积不容异“.意思是两个同高的几何体,如果在等高处的截面积都相等,那么这两个几何体的体积相等.现有某几何体和一个圆锥满足祖暅原理的条件,若该圆锥的侧面展开图是半径为3的圆的三分之一,则该几何体的体积为( )
A.![]() πB.
πB.![]() πC.4
πC.4![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com