
设函数 ,
,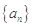

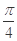
 ,
,

 =
= ,则
,则 ;
;
 .
.
【解析】
试题分析:因为 ,
,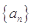
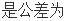
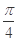
 ,且
,且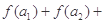
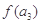 =
=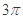 ,
,
设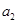 =α,则a1=α-,
=α,则a1=α-,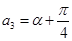 ,
,
由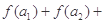
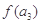 =
=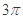 ,
,
得2×3α-[cos+cosα+cos]=3π,
即6α-(+1)cosα=3π.
当0≤α≤π时,左边是α的增函数,且α=满足等式;
当α>π时,6α>6π,而(+1)cosα<3cosα≤3,等式不可能成立;
当α<0时,6α<0,而 (+1)cosα<3,等式也不可能成立.
故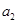 =α=.
=α=.
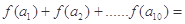 2(
2(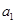 +
+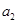 ……+
……+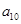 )-(cos
)-(cos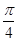 +cos
+cos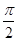 +cos
+cos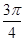 +cosπ+cos
+cosπ+cos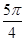 +cos
+cos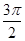 +cos
+cos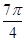 +cos2π+cos
+cos2π+cos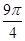 +cos
+cos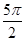 )=
)= .
.
考点:本题主要考查等差数列的通项公式、求和公式,两角和与差的余弦函数,特殊角的三角函数值。
点评:中档题,这是一道根据高考题改编的题目,综合考查等差数列的通项公式、求和公式,两角和与差的余弦函数,特殊角的三角函数值,对考生的分析问题解决问题的能力有较好的考查。


科目:高中数学 来源: 题型:
| x |
| ax-1 |
| 1 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com