
分析 (Ⅰ)求出函数f(x)的导数,通过讨论a的范围,求出函数f(x)的单调区间,从而求出f(x)的最大值即可;
(Ⅱ)设出M的坐标,分别求出直线AB的斜率k1,C在点N处的切线斜率k2,由k1=k2,得到$\frac{l{nx}_{2}-l{nx}_{1}}{{{x}_{1}-x}_{2}}$=-$\frac{2}{{{x}_{1}+x}_{2}}$,得出矛盾.
解答 解:(Ⅰ)f′(x)=$\frac{(2ax+1)(x-1)}{x}$,
当a<0时,由f′(x)=0,得x1=-$\frac{1}{2a}$,x2=1,又x∈[1,2],则有如下分类:
①当-$\frac{1}{2a}$≥2,即-$\frac{1}{4}$≤a<0时,f(x)在[1,2]上是增函数,
所以f(x)max=f(2)=2-ln2.
②当1<-$\frac{1}{2a}$<2,即-$\frac{1}{2}$<a<-$\frac{1}{4}$时,f(x)在[1,-$\frac{1}{2a}$)上是增函数,在(-$\frac{1}{2a}$,2]上是减函数,
所以f(x)max=f(-$\frac{1}{2a}$)=1-$\frac{1}{4a}$+ln(-2a).
③当-$\frac{1}{2a}$≤1,即a≤-$\frac{1}{2}$时,f(x)在[1,2]上是减函数,
所以f(x)max=f(1)=1-a.
综上,函数f(x)在[1,2]上的最大值为:
f(x)max=$\left\{\begin{array}{l}{2-ln2,(-\frac{1}{4}≤a<0)}\\{1-\frac{1}{4a}+ln(-2a),(-\frac{1}{2}<a<-\frac{1}{4})}\\{1-a,(a≤-\frac{1}{2})}\end{array}\right.$;
(Ⅱ)设M(x0,y0),则点N的横坐标为x0=$\frac{{{x}_{1}+x}_{2}}{2}$,
直线AB的斜率k1=$\frac{{{y}_{1}-y}_{2}}{{{x}_{1}-x}_{2}}$=$\frac{1}{{{x}_{1}-x}_{2}}$[a(${{x}_{1}}^{2}$-${{x}_{2}}^{2}$)+(1-2a)(x1-x2)+lnx2-lnx1]
=a(x1+x2)+(1-2a)+$\frac{l{nx}_{2}-l{nx}_{1}}{{{x}_{1}-x}_{2}}$,
C在点N处的切线斜率
k2=f′(x0)=a(x1+x2)+(1-2a)-$\frac{2}{{{x}_{1}+x}_{2}}$,
假设曲线C在点N处的切线平行于直线AB,则k1=k2,
即$\frac{l{nx}_{2}-l{nx}_{1}}{{{x}_{1}-x}_{2}}$=-$\frac{2}{{{x}_{1}+x}_{2}}$,所以ln$\frac{{x}_{2}}{{x}_{1}}$=$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{1+\frac{{x}_{2}}{{x}_{1}}}$,
不妨设x1<x2,$\frac{{x}_{2}}{{x}_{1}}$=t>1,则lnt=$\frac{2(t-1)}{1+t}$,
令g(t)=lnt-$\frac{2(t-1)}{1+t}$(t>1),g′(t)=$\frac{{(t-1)}^{2}}{{t(t+1)}^{2}}$>0,
所以g(t)在(1,+∞)上是增函数,又g(1)=0,
所以g(t)>0,即lnt=$\frac{2(t-1)}{1+t}$不成立,
所以曲线C在点N处的切线不平行于直线AB.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及直线的斜率问题,考查分类讨论思想,换元思想,是一道综合题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
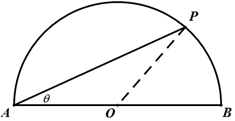 运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.
运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$ | B. | $\frac{25}{8}$ | C. | $\frac{23}{7}$ | D. | $\frac{157}{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | ±$\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x+\sqrt{3}y=2$ | B. | $\sqrt{3}x+y=2$ | C. | $x+\sqrt{3}y=1$ | D. | $\sqrt{3}x+y=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com