过抛物线y2=4x焦点的直线交抛物线于A、B两点,已知|AB|=10,O为坐标原点,则△OAB的重心的坐标是________.
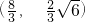
分析:先设A(x
1,y
1),B(x
2,y
2),并将直线设为x=my+1,代入抛物线y
2=4x,运用抛物线定义和韦达定理计算x
1+x
2和y
1+y
2的值,再由重心坐标公式即可得△OAB的重心的坐标
解答:设A(x
1,y
1),B(x
2,y
2),
抛物线y
2=4x焦点坐标为(1,0),准线方程为x=-1
依据抛物线定义,|AB|=x
1+x
2+2=10,∴x
1+x
2=8
设直线方程为x=my+1代入y
2=4x
得y
2-4my-4=0
∴y
1y
2=-4
∵y
12+y
22=(y
1+y
2)
2-2y
1y
2=(y
1+y
2)
2+8=4(x
1+x
2)=32
∴y
1+y
2=±2

△OAB的重心的坐标为(

,
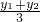
)
故答案为
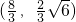
点评:本题考察了抛物线的定义和直线与抛物线的关系,解题时要认真体会抛物线定义和韦达定理在解题中的重要应用,熟记重心坐标公式

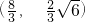

 ,
,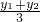 )
)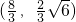


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案