
分析 根据数列的递推关系,得到数列{an}是等差数列,结合等差数列的前n项和公式以及一元二次函数的性质进行求解即可.
解答 解:∵a1=-11,2an=2an-1+3(n≥2),
∴an=an-1+$\frac{3}{2}$,(n≥2),
即an-an-1=$\frac{3}{2}$,
即数列{an}是公差d=$\frac{3}{2}$的等差数列,
则Sn=na1+$\frac{n(n-1)}{2}$d=-11n+$\frac{n(n-1)}{2}$×$\frac{3}{2}$=$\frac{3}{4}$n2-$\frac{47}{4}$n,
对应的抛物线开口向上,对称轴为n=-$\frac{-\frac{47}{4}}{2×\frac{3}{4}}$=$\frac{47}{6}$,
∴当n=8时,Sn取得最小值,最小值为S8=-11×8+$\frac{8×7}{2}$×$\frac{3}{2}$=-88+42=-46,
故答案为:-46;
点评 本题主要考查数列求和的应用,根据条件得到数列{an}是公差d=$\frac{3}{2}$的等差数列,结合一元二次函数的性质是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,3} | B. | {2,4,5} | C. | {1,2,3,4} | D. | {1,2,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a4-3a-2 | B. | a4-$\frac{3}{a}$-2 | C. | a-2 | D. | 4a-$\frac{3}{a}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{3}{4}$ | D. | $\frac{11}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
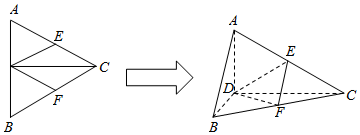
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平均增加2.5千元 | B. | 平均减少2.5千元 | C. | 平均增加3.2千元 | D. | 平均减少3.2千元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com