
【题目】已知函数  的图象上存在不同的两点
的图象上存在不同的两点 ![]() ,使得曲线
,使得曲线 ![]() 在这两点处的切线重合,则实数
在这两点处的切线重合,则实数 ![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】 当 ![]() 时,
时, ![]() 的导数为
的导数为 ![]() ; 当
; 当 ![]() 时,
时, ![]() 的导数为
的导数为 ![]() , 设
, 设 ![]() ,
, ![]() 为该函数图象上的两点,且
为该函数图象上的两点,且 ![]() , 当
, 当 ![]() ,或
,或 ![]() 时,
时, ![]() ,故
,故 ![]() , 当
, 当 ![]() 时,函数
时,函数 ![]() 在点
在点 ![]() 处的切线方程为
处的切线方程为 ![]() ; 当
; 当 ![]() 时,函数
时,函数 ![]() 在点
在点 ![]() 处的切线方程为
处的切线方程为 ![]() . 两直线重合的充要条件是
. 两直线重合的充要条件是 ![]() ①,
①, ![]() ②, 由①及
②, 由①及 ![]() 得
得 ![]() ,由①②得
,由①②得 ![]() , 令
, 令 ![]() ,则
,则 ![]() ,且
,且![]() ,
,
则 ![]() ,结合三次函数的性质可知,
,结合三次函数的性质可知,
![]() 在
在 ![]() 时恒成立,故
时恒成立,故 ![]() 单调递增,即
单调递增,即 ![]() ,
,
即 ![]() ,可得函数
,可得函数 ![]() 的图象在点
的图象在点 ![]() 、
、 ![]() 处的切线重合,
处的切线重合, ![]() 的取值范围是
的取值范围是 ![]() ,故答案为:A.
,故答案为:A.
先根据导数的几何意义分别求出分段函数f(x) 在A、B处的切线方程,再利用两条直线重合的充要条件:斜率相等且纵截距相等列出关系式,从而得出a的代数式,整理后再构造 h(x)对其求导并利用导函数的性质得到 h(x)的单调性和最值,进而得出a的取值范围。


科目:高中数学 来源: 题型:
【题目】如图,给定两个平面单位向量 ![]() 和
和 ![]() ,它们的夹角为120°,点C在以O为圆心的圆弧AB上,且
,它们的夹角为120°,点C在以O为圆心的圆弧AB上,且 ![]() (其中x,y∈R),则满足x+y≥
(其中x,y∈R),则满足x+y≥ ![]() 的概率为( )
的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1的所有棱长都相等,D,E分别是AB,A1C1的中点,如图所示. 
(1)求证:DE∥平面BCC1B1;
(2)求DE与平面ABC所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱AA1的长为5. 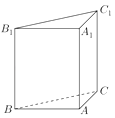
(1)求三棱柱ABC﹣A1B1C1的体积;
(2)设M是BC中点,求直线A1M与平面ABC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目,A、B两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将A队第六位选手的成绩没有给出,并且告知大家B队的平均分比A队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”. 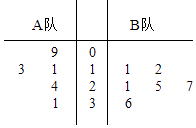
(1)根据茎叶图中的数据,求出A队第六位选手的成绩;
(2)主持人从A队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从A、B两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为ξ,求ξ的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com