设函数f(x)在区间[a，b]上有定义，将区间[a，b]等分成几个小区间，每个小区间的长度为Δx(Δx＝
)，在每个小区间上取一点，依次为x1，x2，…，xi，…，xn．作和Sn＝f(x1)Δx＋f(x2)Δx＋…＋f(xi)Δx＋…＋f(xn)Δx，如果Δx无限趋近于0(亦即n趋向于＋∞)时，Sn无限趋近于常数S，那么称该常数S为函数f(x)在区间[a，b]上的_________，记为S＝_________，其中f(x)称为_________，[a，b]称为_________，a称为_________，b称为_________．
科目：高中数学 来源：2013届新课标高三配套第四次月考文科数学试卷（解析版） 题型：解答题
已知函数f(x)＝
x3＋
x2－ax－a，x∈R，其中a＞0.
（1）求函数f(x)的单调区间；
（2）若函数f(x)在区间(－2,0)内恰有两个零点，求a的取值范围；
（3）当a＝1时，设函数f(x)在区间[t，t＋3]上的最大值为M(t)，最小值为m(t)，记g(t)＝M(t)－m(t)，求函数g(t)在区间[－3，－1]上的最小值.
查看答案和解析>>
科目：高中数学 来源：高考真题 题型：解答题
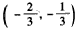内是减函数，求a的取值范围。 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
在区间［0,+∞)上连续,则实数a的值为 .
R.
）内是减函数，求α的取值范围.