
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 由题意和垂直关系可得向量夹角余弦值的方程,解方程结合夹角的范围可得.
解答 解:∵$|\overrightarrow a|=1,|\overrightarrow b|=2$,且$\overrightarrow a⊥(\overrightarrow a-\overrightarrow b)$,
∴$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-$\overrightarrow{a}•\overrightarrow{b}$=1-1×2×cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=0,
解得cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,
∵$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的取值范围是[0,π],
∴向量$\overrightarrow a$和$\overrightarrow b$的夹角<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,
故选:B.
点评 本题考查向量的数量积和夹角以及垂直关系,属基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | ±4$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)有最小值2 | B. | 函数f(x)有最大值2 | C. | 函数f(x)有最小值3 | D. | 函数f(x)有最大值3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0)∪(3,+∞) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
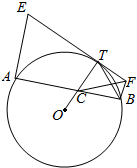 已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:
已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com