Question

5．若等边△ABC的边长为$2\sqrt{3}$，平面内一点M满足$\overrightarrow{CM}=\frac{1}{3}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CA}$，则$\overrightarrow{MA}•\overrightarrow{MB}$等于（　　）

• A． $2\sqrt{3}$
• B． $-2\sqrt{3}$
• C． 2
• D． -2

Answer 1

分析 如图所示，建立直角坐标系．利用向量坐标运算性质、数量积运算性质即可得出．

解答 解：如图所示，建立直角坐标系．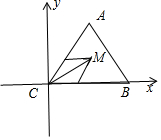
C（0，0），A$（\sqrt{3}，3）$，B$（2\sqrt{3}，0）$．
$\overrightarrow{CA}$=$（\sqrt{3}，3）$，$\overrightarrow{CB}$=$（2\sqrt{3}，0）$．
∴$\overrightarrow{CM}=\frac{1}{3}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CA}$=$\frac{1}{3}$[$（\sqrt{3}，3）$+$（2\sqrt{3}，0）$]=（$\sqrt{3}$，1），
则$\overrightarrow{MA}•\overrightarrow{MB}$=（0，2）•$（\sqrt{3}，-1）$=-2．
故选：D．

点评 本题考查了向量坐标运算性质、数量积运算性质，考查了推理能力与计算能力，属于中档题．