
如图,在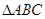 中,
中,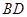 为
为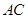 边上的高,
边上的高,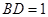 ,
,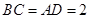 ,沿
,沿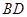 将
将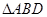 翻折,使得
翻折,使得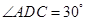 ,得到几何体
,得到几何体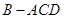 。
。
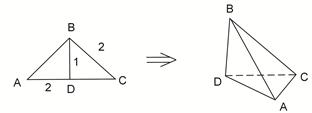
(1)求证: ;
;
(2)求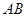 与平面
与平面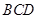 所成角的正切值。
所成角的正切值。
科目:高中数学 来源:2013届吉林长春市高二第二次月考文科数学试卷(解析版) 题型:解答题
如图,在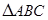 中,
中,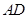 为
为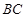 边上的中线,
边上的中线, 为
为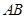 上任意一点,
上任意一点,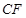 交
交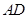 于点
于点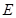 .求证:
.求证: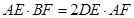 .
.
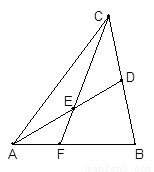
【解析】本试题主要是考查了平面几何中相似三角形性质的运用。根据已知条件,首先做辅助线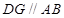 ,然后利用平行性得到相似比,
,然后利用平行性得到相似比,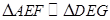 ,
,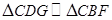 ,然后得到比例相等。充分利用比值问题转化得到结论。
,然后得到比例相等。充分利用比值问题转化得到结论。
证明:过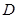 作
作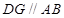 ,交
,交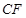 于
于 ,∴
,∴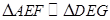 ,
,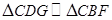 ,
,
∴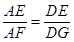 ,
,  , ∵
, ∵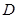 为
为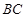 的中点,
的中点,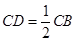 ,
,
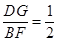 ,
,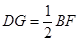 ,
,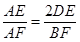 ,即
,即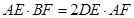 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com