
一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(Ⅰ)从中同时摸出两个球,求两球颜色恰好相同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(1) ;
;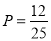 .
.
【解析】
试题分析:(1)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(2)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;(3)注意判断是古典概型还是几何概型,基本事件前者是有限的,后者是无限的,两者都是等可能性.
试题解析:解(Ⅰ)设黑色球记为 ,白色球记为
,白色球记为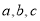 ,摸出两球颜色恰好相同,有
,摸出两球颜色恰好相同,有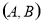 ,
,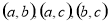 即两个黑球或两个白球,共有4种可能情况.基本事件共有
即两个黑球或两个白球,共有4种可能情况.基本事件共有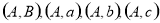 ,
,
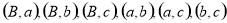 共有10种情况,故所求事件概率
共有10种情况,故所求事件概率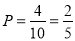 .
.
(Ⅱ)有放回地摸两次,两球颜色不同,即“先黑后白”或“先白后黑”.故事件包括: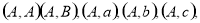

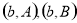
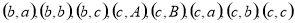 共有25种情况,颜色不同包括:
共有25种情况,颜色不同包括:
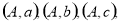
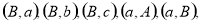
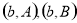
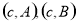 12种情况
12种情况
故所求事件的概率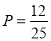 .
.
考点:求随机事件发生的概率.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016届浙江省宁波市高一下学期期末考试数学试卷(解析版) 题型:解答题
设数列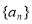 的首项
的首项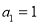 ,前
,前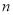 项和为
项和为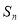 ,且
,且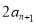 ,
,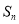 ,
,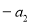 成等差数列,其中
成等差数列,其中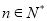 .
.
(1)求数列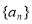 的通项公式;
的通项公式;
(2)数列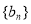 满足:
满足: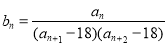 ,记数列
,记数列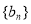 的前
的前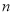 项和为
项和为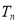 ,求
,求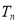 及数列
及数列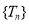 的最大项.
的最大项.
查看答案和解析>>
科目:高中数学 来源:2016届河南长葛第三实验高中高一下学期第三次考试数学试卷(解析版) 题型:选择题
我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为( )
A.45,75,15 B.45,45,45 C.30,90,15 D.45,60,30
查看答案和解析>>
科目:高中数学 来源:2016届河南省实验学校高一下学期期末数学试卷2(解析版) 题型:选择题
将函数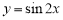 的图象沿x轴方向左平移
的图象沿x轴方向左平移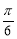 个单位, 则平移后的图象所对应函数的解析式是
个单位, 则平移后的图象所对应函数的解析式是
A.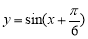 B.
B.
C. D.
D.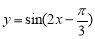
查看答案和解析>>
科目:高中数学 来源:2016届河南省实验学校高一下学期期末数学试卷1(解析版) 题型:选择题
点P是△ABC所在平面内的一点,且满足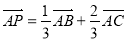 ,则△PAC的面积与△ABC的面积之比为( )
,则△PAC的面积与△ABC的面积之比为( )
A.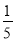 B.
B.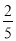 C.
C. D.
D.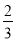
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com