
| x | 2 | 4 | 6 | 8 | 10 |
| y | 5 | 6 | 5 | 9 | 10 |
分析 (1)产量x与相应的生产能耗y的平均数,得到样本中心点,把所给的数据代入公式,利用最小二乘法求出线性回归方程的系数,再求出$\widehata$的值,从而得到线性回归方程;
(2)当x=20,代入回归直线方程,求得$\widehaty$.
解答 解:(1)由题意得$\overline x$=$\frac{2+4+6+8+10}{5}$=6,$\overline y$=$\frac{5+6+5+9+10}{5}$=7,…(1分)
$\sum_{i=1}^5{{x_i}{y_i}}$=2×5+4×6+6×5+8×9+10×10=236,…(3分)
$\sum_{i=1}^5{{x_i}^2}$=4+16+36+64+100=220,…(4分)
则$\widehatb$=$\frac{\sum_{i=1}^{5}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{5}{x}_{i}^{2}-5{\overline{x}}^{2}}$=$\frac{236-5×6×7}{220-5×36}$=0.65,…(6分)
$\widehata$=$\overline y$-$\widehatb$$\overline x$=7-0.65×6=3.1,…(8分)
故线性回归方程为$\widehaty$=0.65x+3.1;…(9分)
(2)根据线性回归方程的预测,现在生产当x=20吨时,产品消耗的标准煤的数量$\widehaty$为:$\widehaty$=0.65×20+3.1=16.1(11分)
答:预测生产20吨甲产品的生产能耗16.1吨标准煤…(12分)
点评 本题考查线性回归方程的求法和应用,解题的关键是正确利用最小二乘法公式,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
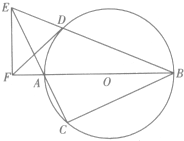 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且满足BD•BE=BA•BF.求证:
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且满足BD•BE=BA•BF.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(-1,0)∪(2,+∞) | B. | (-∞,-2)∪(-1,0)∪(1,+∞) | C. | (-∞,0)∪(1,+∞) | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P甲=P乙 | B. | P甲<P乙 | C. | P甲>P乙 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com