【答案】
分析:(1)设椭圆C上的点P坐标为(x
,y
),可得

=

+

-c
2,根据P是椭圆C上的点,满足

=b
2(1-

),且-a<x
<a,所以

=(1-

)

+b
2-c
2≤b
2,当且仅当

=a
2时,

的最大值为b
2=8,根据椭圆的离心率为

,可算出a
2=12,从而得到椭圆C的方程;
(2)根据△F
1PF
2为等腰三角形,可得点P为直角顶点时,P是短轴顶点;P是锐角顶点时,长轴是焦距的1+

倍.由此计算可得椭圆C的离心率.
解答:解:(1)设椭圆C上的点P坐标为(x
,y
),可得

=(-c-x
,-y
),

=(c-x
,-y
),
∴

=(-c-x
)(c-x
)+

=

+

-c
2∵P是椭圆C上的点,满足

=b
2(1-

),且-a<x
<a
∴

=(1-

)

+b
2-c
2≤(1-

)•a
2+b
2-c
2=b
2所以,当且仅当

=a
2时,

的最大值为b
2=8,可得b=2

∵椭圆的离心率为

,∴

,可得a=

c,b=

c
∴c=2,a=2

,椭圆C的方程是

(2)∵△F
1PF
2为等腰直角三角形,
∴①点P为直角顶点时,P必定是短轴顶点,
OP=

F
1F
2=c,即b=c,

=c,可得a
2=2c
2,即a=

c
∴椭圆C的离心率e=

=

②当某焦点是直角顶点时,
2a=PF
1+PF
2=(1+

)F
1F
2=(1+

)×2c
∴椭圆C的离心率e=

=

=

=

综上所述,该椭圆的离心率e=

-1或

.
点评:本题已知椭圆上一点P满足数量积

的最大值为8,且离心率已知的情况下求椭圆的方程,着重考查了平面向量的数量积和椭圆的基本概念等知识点,属于基础题.

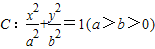 的左右焦点,点P是椭圆C上的动点.
的左右焦点,点P是椭圆C上的动点.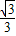 ,且
,且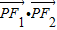 的最大值为8,求椭圆C的方程;
的最大值为8,求椭圆C的方程; =
= +
+ -c2,根据P是椭圆C上的点,满足
-c2,根据P是椭圆C上的点,满足 =b2(1-
=b2(1- ),且-a<x<a,所以
),且-a<x<a,所以 =(1-
=(1- )
) +b2-c2≤b2,当且仅当
+b2-c2≤b2,当且仅当 =a2时,
=a2时, 的最大值为b2=8,根据椭圆的离心率为
的最大值为b2=8,根据椭圆的离心率为 ,可算出a2=12,从而得到椭圆C的方程;
,可算出a2=12,从而得到椭圆C的方程; 倍.由此计算可得椭圆C的离心率.
倍.由此计算可得椭圆C的离心率. =(-c-x,-y),
=(-c-x,-y), =(c-x,-y),
=(c-x,-y), =(-c-x)(c-x)+
=(-c-x)(c-x)+ =
= +
+ -c2
-c2 =b2(1-
=b2(1- ),且-a<x<a
),且-a<x<a =(1-
=(1- )
) +b2-c2≤(1-
+b2-c2≤(1- )•a2+b2-c2=b2
)•a2+b2-c2=b2 =a2时,
=a2时, 的最大值为b2=8,可得b=2
的最大值为b2=8,可得b=2
 ,∴
,∴ ,可得a=
,可得a= c,b=
c,b= c
c ,椭圆C的方程是
,椭圆C的方程是
 F1F2=c,即b=c,
F1F2=c,即b=c, =c,可得a2=2c2,即a=
=c,可得a2=2c2,即a= c
c =
=
 )F1F2=(1+
)F1F2=(1+ )×2c
)×2c =
= =
= =
=
 -1或
-1或 .
. 的最大值为8,且离心率已知的情况下求椭圆的方程,着重考查了平面向量的数量积和椭圆的基本概念等知识点,属于基础题.
的最大值为8,且离心率已知的情况下求椭圆的方程,着重考查了平面向量的数量积和椭圆的基本概念等知识点,属于基础题. 
