
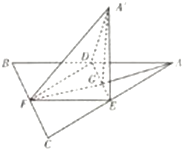
 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,将△ADE绕DE旋转得到△A′DE(A′∉平面ABC),则下列叙述错误的是( )
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,将△ADE绕DE旋转得到△A′DE(A′∉平面ABC),则下列叙述错误的是( )| 1 |
| 3 |
| 1 |
| 2 |
| a |
| 2 |
| ||
| 2×2 |
| ||
| 4 |
| 1 |
| 64 |


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
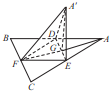 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:| 1 | 64 |
查看答案和解析>>
科目:高中数学 来源:河南省新郑二中分校2009届高三上学期模拟试卷(二)(数学理) 题型:022
如图,边长为a的等边三角形ABC的中线AF与中位线DE相交于G,已知△![]() ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有________.(填上所有正确命题的序号)
ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有________.(填上所有正确命题的序号)
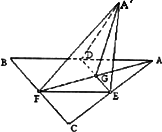
①动点![]() 在平面ABC上的射影在线段AF上;
在平面ABC上的射影在线段AF上;
②异面直线![]() E与BD不可能互相垂直;
E与BD不可能互相垂直;
③恒有平面![]() GF⊥平面BCED;
GF⊥平面BCED;
④三棱锥![]() -FED的体积有最大值.
-FED的体积有最大值.
查看答案和解析>>
科目:高中数学 来源:2014届河南省毕业班阶段测试一理数学卷(解析版) 题型:选择题
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,将△ADE绕DE旋转得到△A′DE(A′ 平面ABC),则下列叙述错误的是(
)
平面ABC),则下列叙述错误的是(
)
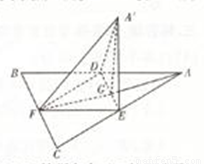
A. 平面A′FG⊥平面ABC
B. BC∥平面A′DE
C. 三棱锥A′-DEF的体积最大值为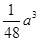
D. 直线DF与直线A′E不可能共面
查看答案和解析>>
科目:高中数学 来源:2014届河南省毕业班阶段测试一文数学卷(解析版) 题型:选择题
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,将△ADE绕DE旋转得到△A′DE(A′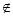 平面ABC),则下列叙述错误的是(
)
平面ABC),则下列叙述错误的是(
)
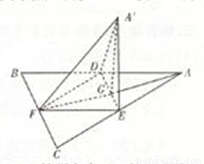
A. 平面A′FG⊥平面ABC
B. BC∥平面A′DE
C. 三棱锥A′-DEF的体积最大值为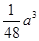
D. 直线DF与直线A′E不可能共面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com