
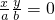 称为椭圆
称为椭圆 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率 .
.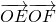 取值范围恰为
取值范围恰为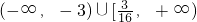 ,求椭圆C的方程.
,求椭圆C的方程. ,得
,得 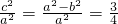 ,
,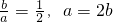 ,椭圆的“特征直线”方程为:x±2y=0.
,椭圆的“特征直线”方程为:x±2y=0.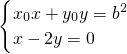 ,解得
,解得 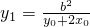 . 同理可求
. 同理可求 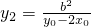 ,
,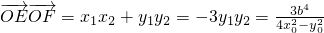 ,∵M(x0,y0)是椭圆上的点,
,∵M(x0,y0)是椭圆上的点,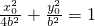 ,从而
,从而  ,
,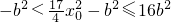 ,∴
,∴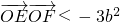 ,或
,或 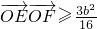 ,
, .
.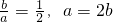 ,即得特征直线
,即得特征直线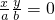 的方程.
的方程.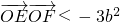 ,或
,或 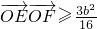 ,结合条件有 b2=1,从而得到 椭圆C的方程.
,结合条件有 b2=1,从而得到 椭圆C的方程.

科目:高中数学 来源:2012-2013学年辽宁省沈阳市高三高考领航考试(一)理科数学试卷(解析版) 题型:解答题
(本小题满分12分,(Ⅰ)小问3分,(Ⅱ)小问9分.)
直线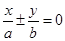 称为椭圆
称为椭圆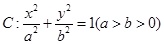 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率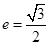 .(1)求椭圆的“特征直线”方程;
.(1)求椭圆的“特征直线”方程;
(2)过椭圆C上一点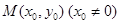 作圆
作圆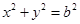 的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若
的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若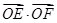 取值范围恰为
取值范围恰为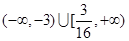 ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省无锡市高二下期中数学试卷(成志班)(解析版) 题型:解答题
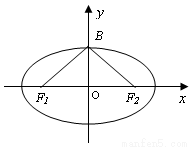
如图,已知椭圆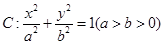 的焦点和上顶点分别为
的焦点和上顶点分别为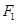 、
、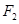 、
、 ,我们称
,我们称 为椭圆
为椭圆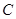 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
(1)已知椭圆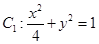 和
和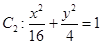 ,判断
,判断 与
与 是否相似,如果相似则求出
是否相似,如果相似则求出 与
与 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)若与椭圆 相似且半短轴长为
相似且半短轴长为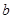 的椭圆为
的椭圆为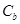 ,且直线
,且直线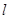 与椭圆为
与椭圆为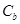 相交于两点
相交于两点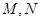 (异于端点),试问:当
(异于端点),试问:当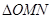 面积最大时,
面积最大时,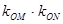 是否与
是否与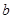 有关?并证明你的结论.
有关?并证明你的结论.
(3)根据与椭圆 相似且半短轴长为
相似且半短轴长为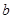 的椭圆
的椭圆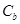 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆八中高三(上)第五次月考数学试卷(理科)(解析版) 题型:解答题
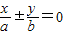 称为椭圆
称为椭圆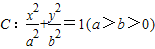 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率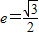 .
.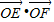 取值范围恰为
取值范围恰为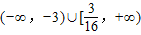 ,求椭圆C的方程.
,求椭圆C的方程.查看答案和解析>>
科目:高中数学 来源:2011年安徽省阜阳市太和县第二职业高级中学高三质量检测数学试卷2(理科)(解析版) 题型:解答题
 称为椭圆
称为椭圆 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率 .
. 取值范围恰为
取值范围恰为 ,求椭圆C的方程.
,求椭圆C的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com