
)已知某音响设备由五个部件组成,A电视机,B影碟机,C线路,D左声道和E右声道,其中每个部件工作的概率如图所示,能听到声音,当且仅当A与B中有一个工作,C工作,D与E中有一个工作;且若D和E同时工作则有立体声效果.
(1)求能听到立体声效果的概率;
(2)求听不到声音的概率.(结果精确到0.01)
(1)0.52;(2)0.13.
解析试题分析:(1)根据事件A,B,C,D,E 的能否正常工作没有影响,即是相互独立事件,又事件A发生的概率为0.9,由对立事件的概率得出事件A不发生的概率为1-0.90,同理事件B不发生的概率为1-0.8,根据独立事件的概率公式可得出能听到立体声效果的概率;(2)事件“听不到声音的”即为“当A、B都不工作,或C不工作,或D、E都不工作时”,又有独立事件的概率公式得出结论..
试题解析:(1)因为A与B中都不工作的概率为 ;
;
所以能听到立体声效果的概率为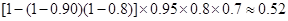 . 6分
. 6分
(2)当A、B都不工作,或C不工作,或D、E都不工作时,就听不到音响设备的声音.
其否定是:A、B至少有1个工作,且C工作,且D、E中至少有一个工作.
所以,听不到声音的概率为 .
.
10分
答:(1) 能听到立体声效果的概率约为0.52;(2)听不到声音的概率为0.13. 12分
考点:互斥事件、对立事件、独立事件的概率.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:解答题
电子蛙跳游戏是:青蛙第一步从如图所示的正方体 顶点
顶点 起跳,每步从一顶点跳到相邻的顶点.
起跳,每步从一顶点跳到相邻的顶点.
(1)求跳三步跳到 的概率
的概率 ;
;
(2)青蛙跳五步,用 表示跳到过
表示跳到过 的次数,求随机变量
的次数,求随机变量 的概率分布及数学期望
的概率分布及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
(Ⅰ)求 ,
,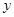 ;
;
(Ⅱ)若从高二、高三年级抽取的人中选 人,求这2人都来自高二年级的概率.
人,求这2人都来自高二年级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某小组共有 、
、 、
、 、
、 、
、 五位同学,他们的身高(单位:米)以及体重指
五位同学,他们的身高(单位:米)以及体重指
标(单位:千克/米2)如下表所示:
| |  |  |  |  |  |
| 身高 |  |  |  |  |  |
| 体重指标 |  |  |  |  |  |
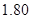 的同学中任选
的同学中任选 人,求选到的
人,求选到的 人身高都在
人身高都在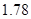 以下的概率;
以下的概率; 人,求选到的
人,求选到的 人的身高都在
人的身高都在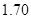 以上且体重指标都在
以上且体重指标都在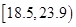 中的概率.
中的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某社区举办防控甲型H7N9流感知识有奖问答比赛,甲、乙、丙三人同时回答一道卫生知识题,三人回答正确与错误互不影响。已知甲回答这题正确的概率是 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是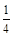 .
.
(I)求乙、丙两人各自回答这道题正确的概率;
(II)用 表示回答该题正确的人数,求
表示回答该题正确的人数,求 的分布列和数学期望
的分布列和数学期望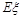 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求:
(Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数 的概率分布列及期望.
的概率分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 | 相关人数 | 抽取人数 |
| A | 18 |  |
| B | 36 | 2 |
| C | 54 | 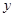 |
 ,
,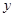 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com