练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)

    (Ⅰ)求,；
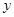    (Ⅱ)若从高二、高三年级抽取的人中选人,求这2人都来自高二年级的概率.

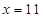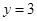    (Ⅰ)，；(Ⅱ) .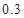

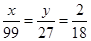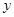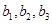    解析试题分析：(Ⅰ)在分层抽样中每层抽取的个体数是按各层个体数在总体的个数中所占的比例抽取的，所以由图可知，，解出和即可；(Ⅱ)先标记从高二年级中抽取的人为，从高三年级抽取的人为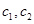，再列举出“从这两个年级中抽取的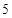人中选人”的所有的基本事件有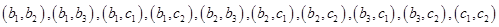：共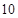种，然后找出满足“选中的人都来自高二”的基本事件有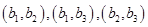：共种，后者除以前者即是所求概率.
    试题解析：(Ⅰ)由题意可知，，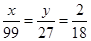
    解得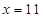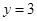，.          4分
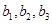    (Ⅱ)记从高二年级中抽取的人为，从高三年级抽取的人为，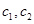
    则从这两个年级中抽取的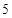人中选人的基本事件有：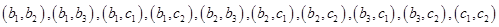
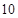    共种，8分
    设选中的人都来自高二的事件为，
    则包含的基本事件有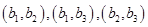：共3种.
    因此，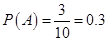
    故选中的人都是来自高二的概率为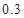.             12分
    考点：1.分层抽样；2.基本事件；3.条件概率

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某项考试按科目A、科目B依次进行，只有当科目A成绩合格时，才可继续参加科目B的考试.已知每个科目只允许有一次补考机会，两个科目成绩均合格方可获得证书.现某人参加这项考试，科目A每次考试成绩合格的概率均为，科目B每次考试成绩合格的概率均为.假设各次考试成绩合格与否均互不影响.
    （1）求他不需要补考就可获得证书的概率；
    （2）在这项考试过程中，假设他不放弃所有的考试机会，记他参加考试的次数为，求 的分布列及数学期望E.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）为迎接2014年“马”年的到来，某校举办猜奖活动，参与者需先后回答两道选择题，问题有三个选项，问题有四个选项，但都只有一个选项是正确的，正确回答问题可获奖金元，正确回答问题可获奖金元，活动规定：参与者可任意选择回答问题的顺序，如果第一个问题回答正确，则继续答题，否则该参与者猜奖活动终止，假设一个参与者在回答问题前，对这两个问题都很陌生.
    （1）如果参与者先回答问题，求其恰好获得奖金元的概率；
    （2）试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    中国航母“辽宁舰”是中国第一艘航母，“辽宁”号以4台蒸汽轮机为动力,为保证航母的动力安全性，科学家对蒸汽轮机进行了170余项技术改进，增加了某项新技术，该项新技术要进入试用阶段前必须对其中的三项不同指标甲、乙、丙进行通过量化检测。假如该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为、、。指标甲、乙、丙合格分别记为4分、2分、4分；若某项指标不合格，则该项指标记0分，各项指标检测结果互不影响。
    (I)求该项技术量化得分不低于8分的概率；
    (II)记该项新技术的三个指标中被检测合格的指标个数为随机变量X,求X的分布列与数学期望。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某公司招聘员工采取两次考试(笔试)的方法：第一试考选择题，共10道题（均为四选一题型），每题10分，共100分；第二试考解答题，共3题。规则是：只有在一试中达到或超过80分者才获通过并有资格参加二试，参加二试的人只有答对2题或3题才能被录用。现有甲、乙两人参加该公司的招聘考试。且已知在一试时：两人均会做10道题中的6道；对于另外4道题来说，甲有两题可排除两个错误答案、有两题完全要猜，乙有两题可排除一个错误答案、有一题可排除两个错误答案、有一题完全要猜。进入二试后，对于任意一题，甲答对的概率是、乙答对的概率是.（1）分别求甲、乙两人能通过一试进入二试的概率、；（2）求甲、乙两人都能被录用的概率.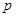

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某幼儿园在“六·一儿童节”开展了一次亲子活动，此次活动由宝宝和父母之一（后面以家长代称）共同完成，幼儿园提供了两种游戏方案：
    方案一 宝宝和家长同时各抛掷一枚质地均匀的正方体骰子（六个面的点数分别是1，2，3，4，5，6），宝宝所得点数记为,家长所得点数记为;
    方案二 宝宝和家长同时按下自己手中一个计算器的按钮(此计算器只能产生区间［1，6］的随机实数)，宝宝的计算器产生的随机实数记为,家长的计算器产生的随机实数记为.
    （Ⅰ）在方案一中，若,则奖励宝宝一朵小红花，求抛掷一次后宝宝得到一朵小红花的概率；
    （Ⅱ）在方案二中，若,则奖励宝宝一本兴趣读物，求按下一次按钮后宝宝得到一本兴趣读物的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    ）已知某音响设备由五个部件组成，A电视机，B影碟机，C线路，D左声道和E右声道，其中每个部件工作的概率如图所示，能听到声音，当且仅当A与B中有一个工作，C工作，D与E中有一个工作；且若D和E同时工作则有立体声效果.

    （1）求能听到立体声效果的概率；
    （2）求听不到声音的概率.（结果精确到0.01）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某工厂三个车间共有工人1000人各车间男、女工人数如表：

    已知在全厂工人中随机抽取1名，抽到第二车间男工的概率是0.15．
    （1）求x的值；
    （2）现用分层抽样的方法在第一、第二、第三车间共抽取60名工人参加座谈分，问应在第三车间抽取多少名？
    （3）已知y≥185，z≥185，求第三车间中女工比男工少的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲，乙，丙三位学生独立地解同一道题，甲做对的概率为，乙，丙做对的概率分别为， (＞)，且三位学生是否做对相互独立.记为这三位学生中做对该题的人数，其分布列为：


    		0
    		1
    		2
    		3





    (Ⅰ)求至少有一位学生做对该题的概率；
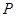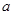    (Ⅱ)求，的值；
    (Ⅲ)求的数学期望.

    查看答案和解析>>

    同步练习册答案