
某工厂三个车间共有工人1000人各车间男、女工人数如表:
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求x的值;
(2)现用分层抽样的方法在第一、第二、第三车间共抽取60名工人参加座谈分,问应在第三车间抽取多少名?
(3)已知y≥185,z≥185,求第三车间中女工比男工少的概率.
(I) ;(II)
;(II)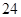 ;(III)
;(III)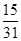 .
.
解析试题分析:(I)总的人数乘以第二车间男工对应的概率即可;(II)根据分层抽样,确定第三车间人数占总人数的百分比,然后乘以60即可;(III)列举出所有可能的结果,用女工比男工少的情况数除以总情况数即可.
试题解析:(I)由题意可知 ,解得
,解得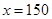 . 3分
. 3分
(II)由题意可知第三车间共有工人数为 名,
名,
则设应在第三车间抽取 名工人,则
名工人,则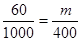 ,
, . 7分
. 7分
(III)由题意可知 ,且
,且 ,满足条件的
,满足条件的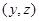 有
有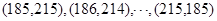 共
共 组, 8分
组, 8分
记“第三车间女工比男工少”为事件 ,即
,即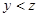 ,上述
,上述 组中,满足
组中,满足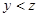 的
的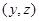 有
有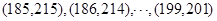 ,共有
,共有 组 9分
组 9分
∴ 11分
11分
故第三车间中女工比男工少的概率为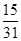 . 12分
. 12分
考点:1、概率的应用;2、分层抽样;3、条件概率.


科目:高中数学 来源: 题型:解答题
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从 三个区中抽取6个工厂进行调查.已知
三个区中抽取6个工厂进行调查.已知 区中分别有27,18,9个工厂.
区中分别有27,18,9个工厂.
(Ⅰ)求从 区中应分别抽取的工厂个数;
区中应分别抽取的工厂个数;
(Ⅱ)若从抽得的6个工厂中随机地抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自 区的概率.
区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
(Ⅰ)求 ,
,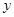 ;
;
(Ⅱ)若从高二、高三年级抽取的人中选 人,求这2人都来自高二年级的概率.
人,求这2人都来自高二年级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某小组共有 、
、 、
、 、
、 、
、 五位同学,他们的身高(单位:米)以及体重指
五位同学,他们的身高(单位:米)以及体重指
标(单位:千克/米2)如下表所示:
| |  |  |  |  |  |
| 身高 |  |  |  |  |  |
| 体重指标 |  |  |  |  |  |
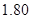 的同学中任选
的同学中任选 人,求选到的
人,求选到的 人身高都在
人身高都在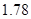 以下的概率;
以下的概率; 人,求选到的
人,求选到的 人的身高都在
人的身高都在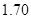 以上且体重指标都在
以上且体重指标都在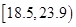 中的概率.
中的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某社区举办防控甲型H7N9流感知识有奖问答比赛,甲、乙、丙三人同时回答一道卫生知识题,三人回答正确与错误互不影响。已知甲回答这题正确的概率是 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是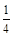 .
.
(I)求乙、丙两人各自回答这道题正确的概率;
(II)用 表示回答该题正确的人数,求
表示回答该题正确的人数,求 的分布列和数学期望
的分布列和数学期望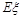 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设有关于x的一元二次方程 .
.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求:
(Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数 的概率分布列及期望.
的概率分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
其市有小型超市72个,中型超市24个,大型超市12个,现采用分层抽样方法抽取9个超市对其销售商品质量进行调查.
(I)求应从小型、中型、大型超市分别抽取的个数;
(II)若从抽取的9个超市中随机抽取3个做进一步跟踪分析,记随机变量X为抽取的小型超市的个数,求随机变量X的分布列及数学期望E(X) .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了调查某大学学生在周日上网的时间,随机对1OO名男生和100名女生进行了不记 名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(II)完成下面的2x2列联表,并回答能否有90%的把握认为“学生周日上网时间与性 别有关”?
表3: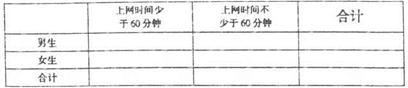

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com