
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从 三个区中抽取6个工厂进行调查.已知
三个区中抽取6个工厂进行调查.已知 区中分别有27,18,9个工厂.
区中分别有27,18,9个工厂.
(Ⅰ)求从 区中应分别抽取的工厂个数;
区中应分别抽取的工厂个数;
(Ⅱ)若从抽得的6个工厂中随机地抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自 区的概率.
区的概率.
(Ⅰ)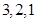 ;(Ⅱ)
;(Ⅱ)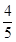
解析试题分析:(Ⅰ)由分层抽样的含义即可得总共有54个工厂,所以抽取的6个工厂占总数的 ,所以每个区域的工厂的个数即可求出.
,所以每个区域的工厂的个数即可求出.
(Ⅱ)因为6个被抽到的工厂中,A区有3个工厂,B区有2个,C区有1个.从中抽取两个工厂共有15种情况,一一列举出来.通过数2个工厂中都没来自 区的共有3种情况,所以符合2个工厂中至少有1个来自
区的共有3种情况,所以符合2个工厂中至少有1个来自 区的共有12种,即可求得结论.
区的共有12种,即可求得结论.
试题解析:解:(Ⅰ)由题可知,每个个体被抽取到得概率为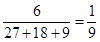 ;
;
设 三个区被抽到的工厂个数为
三个区被抽到的工厂个数为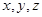 ,则
,则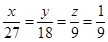
所以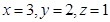 ,故
,故 三个区被抽到的工厂个数分别为
三个区被抽到的工厂个数分别为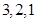
(Ⅱ)设 区抽到的工厂为
区抽到的工厂为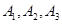 ,
,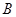 区抽到的工厂为
区抽到的工厂为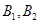 ,
,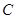 区抽到的工厂为
区抽到的工厂为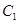
则从6间工厂抽取2个工厂,基本事件有: ,
,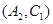 ,
,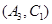 ,
,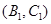 ,
,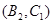 ,
,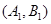 ,
,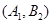 ,
,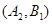 ,
,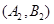 ,
,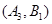 ,
,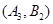
 ,
,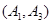 ,
,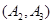 ,
,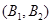 共15种情况;
共15种情况;
2个都没来自 区的基本事件有
区的基本事件有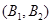 ,
,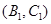 ,
,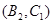 共3种情况
共3种情况
设事件“至少一个工厂来自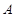 区”为事件
区”为事件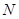 ,则事件
,则事件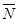 为“2个都没来自
为“2个都没来自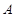 区”
区”
所以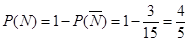
所以,至少有一个工厂来自 区的概率为
区的概率为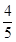
考点:1.分层抽样的思想.2.概率的计算中含至少通常考虑从对立面出发.


科目:高中数学 来源: 题型:解答题
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为 ,求
,求 的分布列及数学期望E
的分布列及数学期望E .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某品牌汽车4 店经销
店经销 三种排量的汽车,其中
三种排量的汽车,其中 三种排量的汽车依次有5,4,3款不同车型.某单位计划购买3辆不同车型的汽车,且购买每款车型等可能.
三种排量的汽车依次有5,4,3款不同车型.某单位计划购买3辆不同车型的汽车,且购买每款车型等可能.
(1)求该单位购买的3辆汽车均为 种排量汽车的概率;
种排量汽车的概率;
(2)记该单位购买的3辆汽车的排量种数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为
次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | 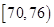 | 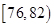 | 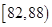 | 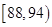 | 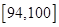 |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)为迎接2014年“马”年的到来,某校举办猜奖活动,参与者需先后回答两道选择题,问题 有三个选项,问题
有三个选项,问题 有四个选项,但都只有一个选项是正确的,正确回答问题
有四个选项,但都只有一个选项是正确的,正确回答问题 可获奖金
可获奖金 元,正确回答问题
元,正确回答问题 可获奖金
可获奖金 元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
(1)如果参与者先回答问题 ,求其恰好获得奖金
,求其恰好获得奖金 元的概率;
元的概率;
(2)试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
中国航母“辽宁舰”是中国第一艘航母,“辽宁”号以4台蒸汽轮机为动力,为保证航母的动力安全性,科学家对蒸汽轮机进行了170余项技术改进,增加了某项新技术,该项新技术要进入试用阶段前必须对其中的三项不同指标甲、乙、丙进行通过量化检测。假如该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为 、
、 、
、 。指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
。指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
(I)求该项技术量化得分不低于8分的概率;
(II)记该项新技术的三个指标中被检测合格的指标个数为随机变量X,求X的分布列与数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂三个车间共有工人1000人各车间男、女工人数如表:
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求x的值;
(2)现用分层抽样的方法在第一、第二、第三车间共抽取60名工人参加座谈分,问应在第三车间抽取多少名?
(3)已知y≥185,z≥185,求第三车间中女工比男工少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
无锡学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设ξ为选出的人中既会唱歌又会跳舞的人数,且P(ξ>0)=
(1)求文娱队的队员人数;
(2)写出ξ的概率分布列并计算E(ξ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com