
 ,
, ,
,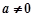 .
. 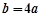 ,求
,求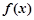 的单调递增区间;
的单调递增区间; 与
与 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且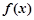 的极小值为
的极小值为 ,求
,求 的值.
的值.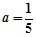 ,
,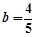 .
.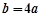 带入函数解析式消b,得到
带入函数解析式消b,得到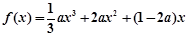 ,对该三次函数求导得到导函数,由于
,对该三次函数求导得到导函数,由于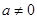 ,故该导函数为二次函数,根据题意需要求的该二次函数大于0的解集,因为二次函数含参数,故依次讨论开口,
,故该导函数为二次函数,根据题意需要求的该二次函数大于0的解集,因为二次函数含参数,故依次讨论开口,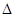 的符号和根的大小,即可到导函数大于0的解集即为原函数的单调增区间.
的符号和根的大小,即可到导函数大于0的解集即为原函数的单调增区间.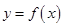 与x轴相切,所以有个极值为0且有一个重根,故可得函数
与x轴相切,所以有个极值为0且有一个重根,故可得函数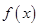 有一个极大值0和一个极小值
有一个极大值0和一个极小值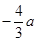 ,有一个重根,则对
,有一个重根,则对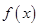 因式分解会得到完全平方式,即
因式分解会得到完全平方式,即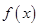 提取x的公因式后,剩下二次式的判别
提取x的公因式后,剩下二次式的判别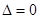 ,得到a,b之间的关系式,再根据极小值为
,得到a,b之间的关系式,再根据极小值为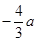 ,则求导求出极小值点,得到关于a,b的另外一个等式,即可求出a,b的值.
,则求导求出极小值点,得到关于a,b的另外一个等式,即可求出a,b的值.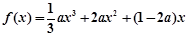 ,
,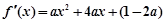 .
.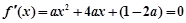 ,
,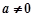 ,
,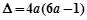
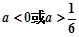 时,由
时,由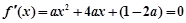 得
得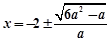 .
.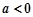 时,
时,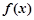 的单调递增区间为
的单调递增区间为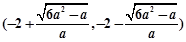 ; 3分
; 3分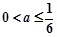 时,
时,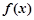 的单调递增区间为
的单调递增区间为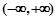 ; 5分
; 5分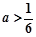 时,
时,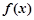 的单调递增区间为
的单调递增区间为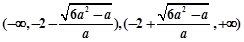 . 7分
. 7分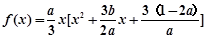 ,
, 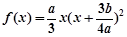 ,且
,且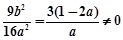 ① 9分
① 9分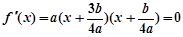 ,得
,得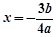 或
或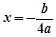 . 11分
. 11分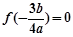 ,所以极小值为
,所以极小值为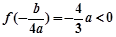 ,
,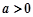 且
且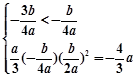 ,得
,得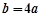 , 13分
, 13分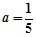 ,
,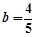 . 15分
. 15分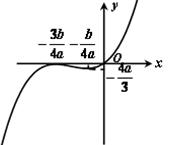


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源:不详 题型:解答题
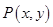 为函数
为函数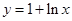 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线 的斜率
的斜率 .
.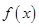 在区间
在区间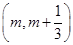
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;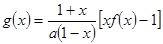 ,若对任意
,若对任意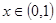 恒有
恒有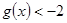 ,求实数
,求实数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com