
已知直线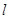 过点
过点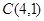 , (1)若直线
, (1)若直线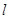 在两坐标轴上截距相等,求直线
在两坐标轴上截距相等,求直线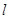 的方程。
的方程。
(2)若直线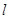 分别与
分别与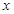 轴、y轴的正半轴相交于
轴、y轴的正半轴相交于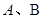 两点,O为坐标原点,记
两点,O为坐标原点,记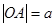
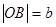 ,求
,求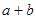 的最小值,并写出此时直线
的最小值,并写出此时直线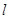 的方程。
的方程。
(1) 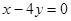 或
或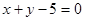 (2)
(2)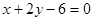
【解析】本题考查的知识点是直线的截距式方程,其中(1)的关键是分析出直线l在两坐标轴上的截距相等包括两种情况,一是过原点,一是斜率为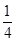 ,在解答时,易忽略直线l过原点这种情况,而错解为x+y-5=0.
,在解答时,易忽略直线l过原点这种情况,而错解为x+y-5=0.
(1)直线l在两坐标轴上的截距相等包括两种情况,一是过原点,一是斜率为1/4,分别求出两种情况下直线l的方程,进而得到答案;
(2) 设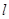 的方程为:
的方程为: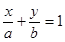 ,
,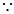 直线
直线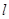 过点
过点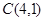 ,
,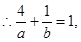 (1)
(1)
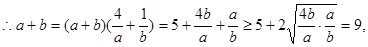 结合不等式性质得到结论。
结合不等式性质得到结论。
解:(1)若直线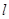 过原点,设其方程为:
过原点,设其方程为: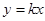 ,又直线
,又直线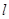 过点
过点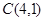 ,则
,则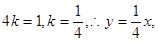 即
即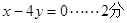
若直线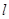 不过原点,设其方程为:
不过原点,设其方程为: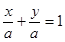 ,
,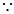 直线
直线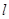 过点
过点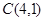 ,
,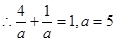
直线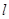 的方程为
的方程为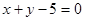 ;综上,
;综上,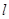 的方程为
的方程为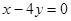 或
或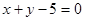
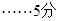
(2)设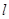 的方程为:
的方程为: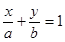 ,
,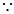 直线
直线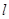 过点
过点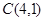 ,
,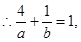 (1)
(1)
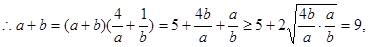 当且仅当
当且仅当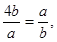
即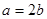 时取等号,将
时取等号,将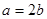 与(1)式联立得
与(1)式联立得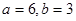 ,
,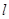 的方程为
的方程为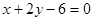
综上,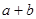 的最小值为9,
的最小值为9,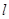 的方程为
的方程为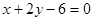 ------------10分
------------10分


科目:高中数学 来源: 题型:
(坐标系与参数方程选做题) 在极坐标系中,已知直线过点(1,0),且其向上的方向与极轴的正方向所成的最小正角为![]() ,则直线的极坐标方程为______________.
,则直线的极坐标方程为______________.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高一下学期期中考试数学试卷(解析版) 题型:解答题
已知直线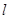 过点
过点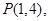
(1)若直线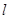 在坐标轴上的截距相等,求直线
在坐标轴上的截距相等,求直线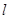 的方程;
的方程;
(2)若直线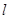 与坐标轴的正半轴相交,求使直线
与坐标轴的正半轴相交,求使直线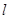 在两坐标轴上的截距之和最小时,直线
在两坐标轴上的截距之和最小时,直线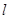 的方程。
的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com