
分析 由根式与绝对值的意义结合方程求出x,y的值判断①;分别求出两函数的值域判断②;由交集运算结合反例判断③.
解答 解:对于①,$\sqrt{x-2}$≥0且|y+2|≥0,若$\sqrt{x-2}$+|y+2|=0,则x=2,y=-2,∴$\sqrt{x-2}$+|y+2|=0的解集为{(2,-2)},①错误;
对于②,由y=x2-1≥-1,得{y|y=x2-1,x∈R}=[-1,+∞),而{y|y=x-1,x∈R}=R.
∴集合{y|y=x2-1,x∈R}与{y|y=x-1,x∈R}的公共元素所组成的集合是[-1,+∞),②错误;
对于③,集合{x|x-2>0}=(2,+∞),当m=3时,集合{x|x-2>0}与集合{x|x<m,m∈R}有公共元素,③错误.
∴不正确的是①②③.
故答案为:①②③.
点评 本题考查命题的真假判断与应用,考查了集合间的关系及其运算,考查了函数值域的求法,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
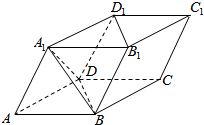 如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).
如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
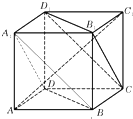 如图正方体ABCD-A1B1C1D1中,下列结论中正确的序号是①③.
如图正方体ABCD-A1B1C1D1中,下列结论中正确的序号是①③.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
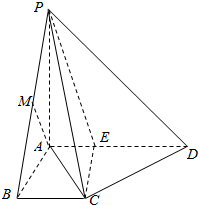 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
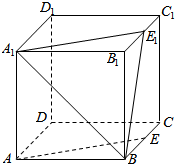 在棱长为1的正方体ABCD-A1B1C1D1中,E、E1分别是BC和B1C1中点,则:
在棱长为1的正方体ABCD-A1B1C1D1中,E、E1分别是BC和B1C1中点,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com