练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
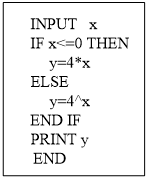
    11．运行如图程序，可求得f（-3）+f（2）的值为4．

    分析 模拟程序语言的运行过程，即可得出该程序的功能是输出函数y=$\left\{\begin{array}{l}{4x}&{x≤0}\\{{4}^{x}}&{x＞0}\end{array}\right.$，代入计算即可得解．

    解答 解：模拟程序语言的运行过程，得出该程序的功能是计算并输出函数y=$\left\{\begin{array}{l}{4x}&{x≤0}\\{{4}^{x}}&{x＞0}\end{array}\right.$的值，
    由于：f（-3）=4×（-3）=-12，f（2）=42=16，
    所以：f（-3）+f（2）=-12+16=4．
    故答案为：4．

    点评 本题利用程序代码考查了分段函数的求值问题，解题时应根据变量x的值选择正确的分支，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=ln（x2+1），g（x）=$\frac{1}{{x}^{2}-1}$+a．
    （1）求g（x）在P（$\sqrt{2}$，g（$\sqrt{2}$））处的切线方程l；
    （2）求方程f（x）=g（x）的根的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．下列有关命正确的是（　　）
    A．命题“若x2=1则x=1”的否命题为“若x2=1，则x≠1”
    B．“x=-1是x2-5x-6=0”必要不充分条件
    C．命题“?x∈（1，+∞），使是x2+x-1＜0”的否定是：“?x∈（1，+∞），均有x2+x-1≥0”
    D．命题“已知x，y∈R，若x≠1，或y≠4则x+y≠5”为真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．函数y=cos（x+$\frac{π}{4}$）的一个单调增区间是（　　）
    A．[-$\frac{π}{2}，\frac{π}{2}}$]B．[$\frac{π}{2}，\frac{3π}{4}}$]C．[$\frac{3π}{4}，π}$]D．[π，2π]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=4x3-3x2cosθ+$\frac{3}{16}$cosθ，其中x∈R，θ为参数，且0＜θ＜$\frac{π}{2}$．
    （Ⅰ）求参数θ的取值范围，使函数f（x）的极小值大于零；
    （Ⅱ）若对于（1）中的任意θ，函数f（x）在区间（2a-1，a）内都是增函数，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设函数y=sin（ωx+φ）（ω＞0，φ∈（-$\frac{π}{2}$，$\frac{π}{2}$））的最小正周期为π，且其图象关于直线x=$\frac{π}{12}$对称，则在下面结论中：
    ①图象关于点（$\frac{π}{6}$，0）对称； 
    ②图象关于点（$\frac{π}{3}$，0）对称；
     ③在[0，$\frac{π}{6}$]上是增函数；
    ④在[-$\frac{π}{3}$，$\frac{π}{12}$]上是增函数；
    ⑤由f（x1）=f（x2）=0可得x1-x2必是π的整数倍．
    正确结论的编号为②④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知直线x-y+1=0上有两点A，B，且AB=2，动点P在抛物线y2=2x上，则△PAB面积的最小值是$\frac{\sqrt{2}}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．在以下四组函数中，表示同一个函数的是（　　）
    A．f（x）=x+1，$g（x）=\frac{{x（{x+1}）}}{x}$B．f（x）=1，$g（x）=\frac{x}{|x|}$C．y=|x|，$y=\sqrt{x^2}$D．$f（x）=\sqrt{x^2}+1$，g（x）=x+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

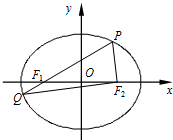    1．如图，在平面直角坐标系xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1，F2，P为椭圆上一点（在x轴上方），连结PF1并延长交椭圆于另一点Q，设$\overrightarrow{P{F}_{1}}$=λ$\overrightarrow{{F}_{1}Q}$．
    （1）若点P的坐标为 （1，$\frac{3}{2}$），且△PQF2的周长为8，求椭圆C的方程；
    （2）若PF2垂直于x轴，且椭圆C的离心率e∈[$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$]，求实数λ的取值范围．

    查看答案和解析>>

    同步练习册答案