
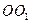 内有一个三棱柱
内有一个三棱柱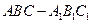 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱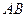 是圆
是圆 的直径。
的直径。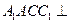 平面
平面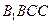 ;
;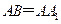 ,在圆
,在圆 柱
柱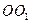 内随机选取一点,记该点取自三棱柱
内随机选取一点,记该点取自三棱柱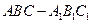 内的概率为
内的概率为 。
。 在圆周上运动时,求
在圆周上运动时,求 的最大值;
的最大值; 与平面
与平面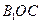 所成的角为
所成的角为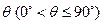 。当
。当 取最大值时,求
取最大值时,求
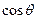 的值。
的值。科目:高中数学 来源:不详 题型:单选题
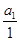 =
=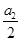 =
=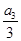 =k,则
=k,则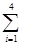 (ihi)=
(ihi)=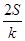 .类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若
.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若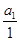 =
=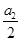 =
=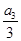 =K,则
=K,则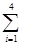 (ihi)=( )
(ihi)=( ) A. | B.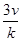 | C.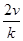 | D.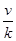 |
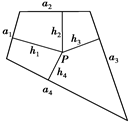
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.30° | B.45° | C. 75° | D.60° |
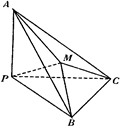
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
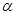 ,
,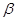 ,
,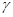 两两互相垂直,点
两两互相垂直,点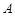 ∈
∈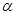 ,点
,点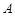 到
到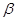 ,
,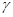 的距离都是
的距离都是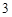 ,点
,点 是
是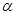 上的动点,满足
上的动点,满足 到
到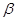 的距离是到
的距离是到 到点
到点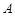 距离的
距离的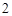 倍,则点
倍,则点 的轨迹上的点到
的轨迹上的点到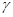 的距离的最小值是
的距离的最小值是A.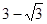 | B.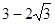 |
C.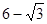 | D.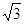 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
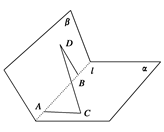
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com