正数等差数列{an},若存在常数t,使得a2n=tan,对一切n∈N*均成立,则t可能取的值是( )
A.1
B.2
C.1或2
D.1或3
【答案】
分析:根据等差数列通项公式,将“若存在常数t,使得a
2n=ta
n,对一切n∈N
*均成立”,转化成(2d-td)n+(1-t)(a
1-d)=0 对一切n∈N
*均成立问题解决.
解答:解:{a
n}是正数等差数列,a
2n=ta
n 那么根据等差数列通项公式可得a
1+(2n-1)d=t[a
1+(n-1)d],移向化简并整理得(2d-td)n+(1-t)(a
1-d)=0 对一切n∈N
*均成立.
∴
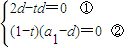
由①得,t=2,此时结合②,a
1=d≠0,数列的通项公式为a
n=nd,符合题意.
由②得,t=1,结合①d=0,数列的通项公式an=a1 数列为正数常数列,符合题意.
所以t可能取的值是 1,2
故选C.
点评:本题考查在数列背景下的等式恒成立的条件.转化成(2d-td)n+(1-t)(a
1-d)=0 对一切n∈N
*均成立是关键.要注意验证t的取值是否使得数列存在.

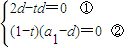 由①得,t=2,此时结合②,a1=d≠0,数列的通项公式为an=nd,符合题意.
由①得,t=2,此时结合②,a1=d≠0,数列的通项公式为an=nd,符合题意.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案