Question

（1）已知函数y＝ln（－x²＋x－a）的定义域为（－2,3），求实数a的取值范围；

（2）已知函数y＝ln（－x²＋x－a）在（－2,3）上有意义，求实数a的取值范围．

 

Answer 1

【答案】

（1）-6  （2）a≤－6

【解析】

试题分析：（1）因为，函数y＝ln（－x²＋x－a）的定义域为（－2,3），所以，－x²＋x－a>0的解集为（－2,3），-2，3是方程－x²＋x－a=0的根，故a=-6。

（2）因为，函数y＝ln（－x²＋x－a）在（－2,3）上有意义，即－x²＋x－a>0在（－2,3）成立，而二次函数－x²＋x－a的图象开口向下，对称轴为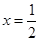，所以，－3²＋3－a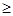0，故a≤－6。

考点：对数函数的性质，一元二次不等式的解法，二次函数的图象和性质。

点评：中档题，本题以对比的形式，给出在不同要求下，此类问题的解法，同时注重了基础性。对于一元二次问题，往往借助于二次函数的图象和性质，数形结合。